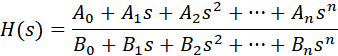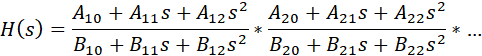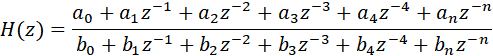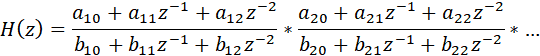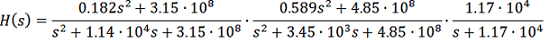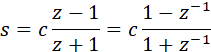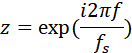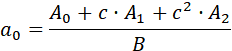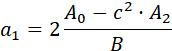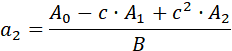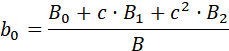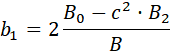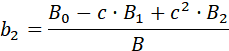Здесь мы рассматриваем класс рекурсивных фильтров или по-другому фильтров с бесконечной импульсной характеристикой (БИХ). Существует множество вариантов реализации рекурсивных фильтров. Самая очевидная – это прямая форма реализации, расчёт которой изложен на странице «Расчёт рекурсивных цифровых фильтров. Прямая реализация». Однако, она не самая простая с точки зрения расчётов. В этом смысле наиболее простая форма реализации рекурсивных фильтров – каскадная форма реализации, на рассмотрении которой мы здесь остановимся. При этом мы будем использовать подход, который заключается в переходе от аналогового фильтра прототипа к цифровому. Из теории известно, что аналоговый фильтр, обобщённая передаточная характеристика которого описывается рациональной функцией следующего вида:
где A и
B- вещественные коэффициенты,
можно представить в виде произведения звеньев второго порядка:
Аналогично цифровой фильтр с обобщённой передаточной характеристикой вида:
где a и b также вещественный коэффициенты, z-k=e-i2πkf/fs , fs-частота дискретизации,
можно представить в виде произведения звеньев второго порядка:
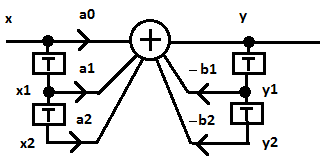
Каждому звену второго порядка соответствует структурная схема вида:
Следовательно, из данных звеньев можно реализовать фильтр любого порядка. Причем, если порядок фильтра n – четный, то звеньев будет n/2. Если n - нечетный, например n=5, то все равно будет три звена, одно из которых, будет соответствовать аналоговому звену 1-го порядка. T – элемент задержки на один период дискретизации. При реализации на вычислительных устройствах работа одного звена фильтра реализуется следующим выражением:
y = a0*x+a1*x1+a2*x2 - b1*y1- b2*y2
Здесь a0 соответствует a0 и т.д. Обозначение x1 соответствует задержки x на 1 период дискретизации, x2 - на 2 периода и т.д. Для y1,y2… аналогично. Звёздочка * означает умножение.
Переходим к расчету цифрового фильтра. Один из распространённых подходов проектирования цифровых фильтров (ЦФ) заключается в пересчёте коэффициентов передаточной функции аналогового фильтра-прототипа (АФ) в коэффициенты цифрового фильтра. Один из методов - метод билинейного преобразования. Он позволяет получить амплитудно-частотную характеристику (АЧХ) ЦФ, максимально близкую к АЧХ АФ-прототипа. Проектированию аналоговых фильтров посвящено много специальной литературы, поэтому данную тему мы пропускаем. Мы спроектируем цифровой фильтр нижних частот (ФНЧ) 5-го порядка и приведём программу расчета конкретного фильтра, которую можно обобщить на фильтры любого типа (Баттерворта, Чебышева, Бесселя и др.) и произвольного порядка.
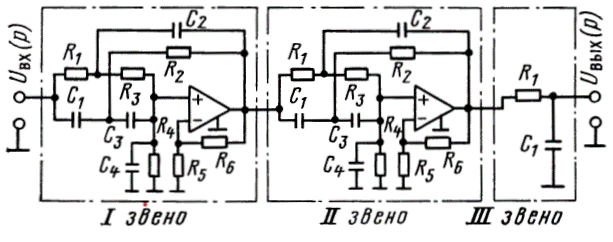
Примем в качестве прототипа конкретный аналоговый фильтр 5-го порядка на частоту среза 3.4 кГц [2]. Схема аналогового ФНЧ-3.4:
Однако нас больше интересует его передаточная характеристика, которая в наших обозначениях имеет следующий вид:
Задача расчёта цифрового фильтра заключается в следующих переходах:
s à z, Ak à ak, Bk à bk для каждого звена
Основная формула билинейного преобразования s à z, выглядит следующим образом [1]:
fs=1/T – частота дискретизации.
Из теории известно, что yмножение в частотной области на z-1 эквивалентно задержки отсчёта на время T во временной области, откуда становиться понятным взаимосвязь приведенных выше выражений для H(z) и y.
Значение коэффициента c непосредственно в билинейной формуле равно c=2/T=2fs. Однако при этом АЧХ ЦФ и АЧХ АФ заметно «разбегаются» с увеличением частоты. Поэтому с целью коррекции стали применять его в следующих вариантах [3]:
Мы определились с заменой s à z. Теперь переходим к преобразованию коэффициентов:
Ak à ak, Bk à bk
В общем случае для звена второго порядка справедливы следующие формулы пересчёта:
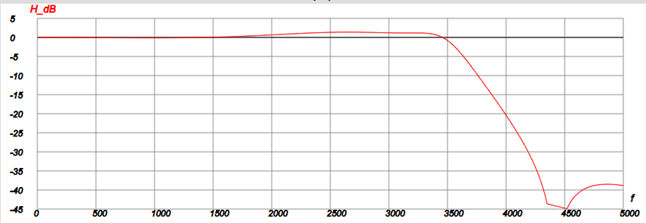
Программа пересчёта, которая выполнима на калькуляторе КАН, приведена в Приложении. Полученный график АЧХ фильтра показан ниже
Видим, что АЧХ соответствует ожидаемой. Для того чтобы пересчитать фильтр на другую частоту fс1, необходимо fc умножить на коэффициент fс1/3400. При этом частота дискретизации fs должна быть в несколько раз выше частоты среза.
Mathcad-программа расчета данного фильтра доступна здесь. Программу нетрудно модифицировать для фильтра любого порядка. Литература и ссылки
2. О.В.Кустов, В.З.Лундин. Операционные усилители в линейных цепях. Москва «Связь» 1978. 3. Phuoc Si Nguyen. Bilinear z-transformation and Pascal’s triangle.
Приложение.;расчет цифрового
рекурсивного фильтра нижних частот
|