| На главную ↑ Выше |
Меандр |
В радиотехнике часто используется сигнал, называемый меандром. Меандр - это последовательность прямоугольных импульсов со скважностью 2 и обычно без постоянной составляющей.
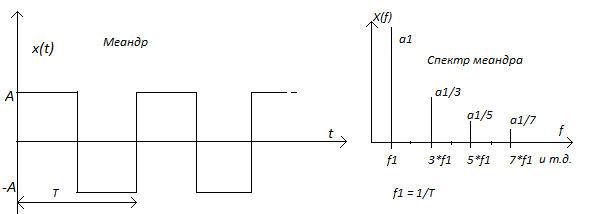 |
Спектр такого сигнала состоит из нечётных гармоник:
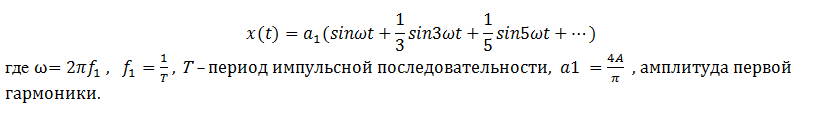 |
Из этого следует неочевидный на первый взгляд вывод, что прямоугольный сигнал можно получить, суммируя синусоидальные сигналы (задача синтеза сигналов). Чтобы в этом убедиться произведём синтез меандра из пяти гармоник, с номерами 1, 3, 5, 7, 9. Скопируем в калькулятор следующую программу.
; программа синтеза меандра по первым 5-ти гармоникам
f1 = 10 ; частота первой гармоники
fd = 1000 ; частота дискретизации
w1 = 2*pi*f1/fd ; относительная круговая частота первой гармоники
a1 = 4/pi ; амплитуда первой гармоники
; основной цикл
t = 0
[
x1 = sin(w1*t); 1-я гармоника
x3 = 1/3*sin(3*w1*t) ; 3-я гармоника
x5 = 1/5*sin(5*w1*t) ; 5-я гармоника
x7 = 1/7*sin(7*w1*t) ; 7-я гармоника
x9 = 1/9*sin(9*w1*t) ; 9-я гармоника
x_sum = a1*(x1 + x3 + x5 + x7 + x9) ; сумма гармоник
val(t,x_sum); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
f1 = 10 ; частота первой гармоники
fd = 1000 ; частота дискретизации
w1 = 2*pi*f1/fd ; относительная круговая частота первой гармоники
a1 = 4/pi ; амплитуда первой гармоники
; основной цикл
t = 0
[
x1 = sin(w1*t); 1-я гармоника
x3 = 1/3*sin(3*w1*t) ; 3-я гармоника
x5 = 1/5*sin(5*w1*t) ; 5-я гармоника
x7 = 1/7*sin(7*w1*t) ; 7-я гармоника
x9 = 1/9*sin(9*w1*t) ; 9-я гармоника
x_sum = a1*(x1 + x3 + x5 + x7 + x9) ; сумма гармоник
val(t,x_sum); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
Получим следующую картину:
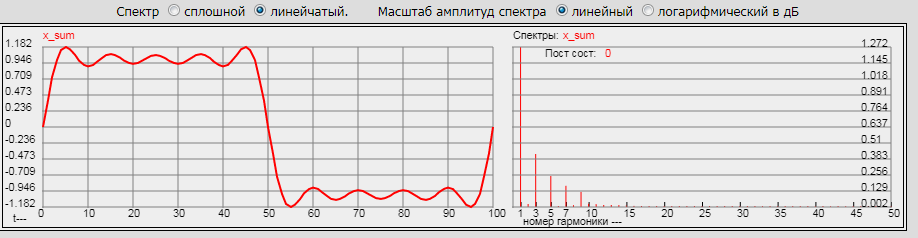 |
Мы получили почти прямоугольный сигнал с амплитудой равной 1. Если количество гармоник увеличивать и дальше по указанному закону, получим прямоугольный периодический сигнал со скважностью 2, который в радиотехнике принято называть меандром.
Один важный момент: частота дискретизации (а мы рассматриваем дискретные модели сигналов) должна быть как минимум в 2 раза выше частоты верхней гармоники составного сигнала. В данном примере, где f9 = 90, а fd = 1000, это соблюдается.
Таким же путём из суммы синусоидальных сигналов можно получить любой другой сигнал (синтез, обратное преобразование Фурье) и, наоборот, любой сигнал можно представить суммой синусоидальных сигналов (спектральный анализ, прямое преобразование Фурье).

|
Обратная связь: alexander.nekhaev53@gmail.com |

|
Поддержать проект |

|
Заказать расчет |