| На главную ↑ Выше |
Расчёт и моделирование цифрового фильтра 1-го порядка
|
На рисунке показана общая схема цифрового (дискретного) фильтра 1-го порядка.
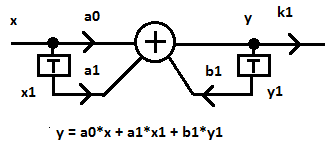 |
Здесь Т – элемент задержки на один период дискретизации,
a0, a1, b1 – коэффициенты фильтра,
k1 – нормирующий коэффициент (например, для того чтобы установить общее
единичное усиление на нулевой частоте).
При a0=1, a1 = 1, b1<1 – данный фильтр становится цифровым аналогом
интегрирующей RC – цепочки.
На следующем рисунке показаны RC-цепочка и её цифровой аналог:
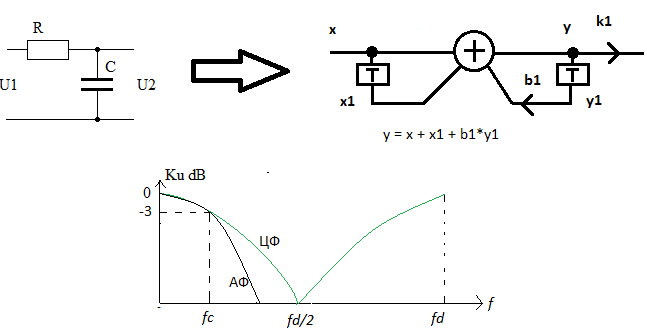 |
В отличие от аналогового фильтра амплитудно-частотная характеристика (АЧХ) цифрового
всегда является периодической с периодом равным частоте дискретизации fd = 1/T.
Поэтому частоту дискретизации перед аналого-цифровым преобразованием выбирают как минимум вдвое
больше верхней частоты аналогового сигнала.
Выбором fd и расчётами можно добиться, чтобы АЧХ цифрового фильтра практически полностью
соответствовала АЧХ аналогового фильтра до определённой частоты fc.
Расчёт
Порядок расчёта параметров фильтра:1. Задаём частоту дискретизации fd
2. Задаём частоту среза цифрового фильтра на уровне 0.707 (-3 дБ) - fc
3. Копируем расчётный текст из Расчётного блока в буфер
4. Запускаем калькулятор
5. Копируем из буфера расчётный текст в окно калькулятора
6. Нажимаем кнопку вычислить и получаем результат:
Расчётный блок:
; расчет и моделирование цифрового фильтра первого порядка
; аналога интегрируюшей RC - цепочки
;================== расчёт =====================
;-------------- задаваемые параметры ----------------
fd = 1000 ; частота дискретизации
fc_dig = 20 ; частота среза цифрового фильтра
;------------- промежуточные расчёты ----------------
fc_an = (fd/pi)*tg(pi*fc_dig/fd)
g = fd/(pi*fc_an)
;------------ расчётные параметры фильтра 1-го порядка --
b1 = - (1 - g)/(1 + g)
k1 = 1/(1 + g)
val(b1,k1): b1 = 0.88162, k1 = 0.05919
;=================== моделирование ================
f = 20 ; частота входного сигнала
w = 2*pi*f/fd
x1 = 0
y1 = 0
;-------------- основной цикл -----------------
t = 0 ; дискретное время(номер отсчёта)
[
x = sin(w*t) ; входной сигнал
y = x + x1 + b1*y1
x1 = x
y1 = y
y_out = k1*y ; выходной сигнал после нормировки
val(t,x,y_out)
t = t + 1
{t>100 exit}
]
; аналога интегрируюшей RC - цепочки
;================== расчёт =====================
;-------------- задаваемые параметры ----------------
fd = 1000 ; частота дискретизации
fc_dig = 20 ; частота среза цифрового фильтра
;------------- промежуточные расчёты ----------------
fc_an = (fd/pi)*tg(pi*fc_dig/fd)
g = fd/(pi*fc_an)
;------------ расчётные параметры фильтра 1-го порядка --
b1 = - (1 - g)/(1 + g)
k1 = 1/(1 + g)
val(b1,k1): b1 = 0.88162, k1 = 0.05919
;=================== моделирование ================
f = 20 ; частота входного сигнала
w = 2*pi*f/fd
x1 = 0
y1 = 0
;-------------- основной цикл -----------------
t = 0 ; дискретное время(номер отсчёта)
[
x = sin(w*t) ; входной сигнал
y = x + x1 + b1*y1
x1 = x
y1 = y
y_out = k1*y ; выходной сигнал после нормировки
val(t,x,y_out)
t = t + 1
{t>100 exit}
]
Подставляя новые задаваемые параметры fd и fc_dig, получаем новые результаты.
Помимо параметров фильтра будет выведена таблица значений входного x и выходного
y_out сигнала
В графическом окне калькулятора будет показан график входного x и выходного y_out сигналов.
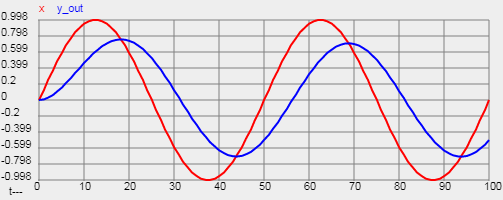 |
Видно, что при частоте 20 Гц амплитуда на выходе равна приблизительно 0.7.
Кроме этого, виден запаздывающий фазовый сдвиг выходного сигнала относительно входного.

|
Обратная связь: alexander.nekhaev53@gmail.com |

|
Поддержать проект |

|
Заказать расчет |