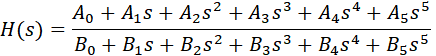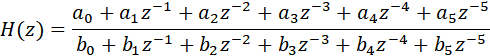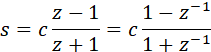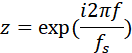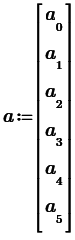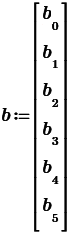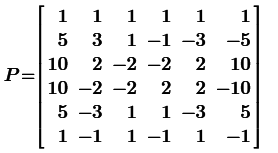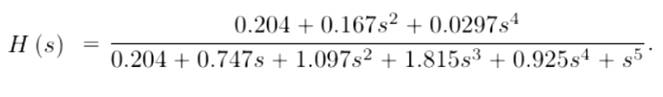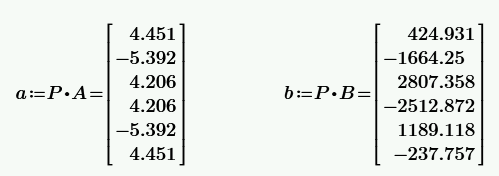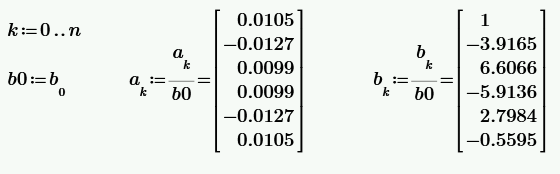Здесь мы рассматриваем класс рекурсивных фильтров или по-другому фильтров с бесконечной импульсной характеристикой (БИХ). Существует множество вариантов реализации рекурсивных фильтров. Самая очевидная – это прямая форма реализации, на которой мы здесь остановимся. Один из распространённых подходов проектирования цифровых фильтров (ЦФ) заключается в пересчёте коэффициентов передаточной функции аналогового фильтра-прототипа (АФ) в коэффициенты цифрового фильтра. Один из методов - метод билинейного преобразования. Он позволяет получить амплитудно-частотную характеристику (АЧХ) ЦФ, аналогичную АЧХ АФ-прототипа. Проектированию аналоговых фильтров посвящено много специальной литературы, поэтому данную тему мы пропускаем. Мы спроектируем цифровой фильтр нижних частот (ФНЧ) 5-го порядка и приведём программу расчета конкретного фильтра, которую можно обобщить на фильтры любого типа (Баттерворта, Чебышева, Бесселя и др.) и произвольного порядка. Обобщенная передаточная функция аналогового звена 5-го порядка имеет вид:
где A и
B- вещественные коэффициенты,
В свою очередь при расчёте аналогового ФНЧ за основу берут передаточную характеристику т.н. нормированного фильтра-прототипа, такого для которого срез имеет место при Ω = 1, где Ω - т.н. нормированная (и следовательно безразмерная) частота:
При этом при расчете передаточной характеристики нормированного фильтра принимается s=iΩ.
Обобщенная передаточная характеристика цифрового фильтра 5-го порядка имеет вид:
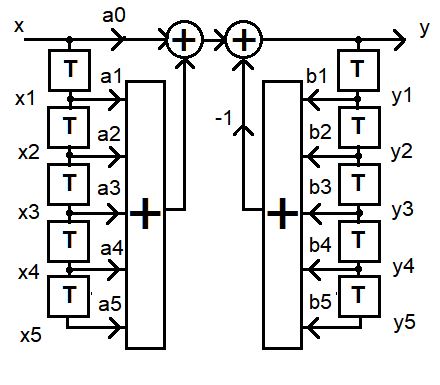
Где z-k=e-i2πkf/fs , fs-частота дискретизации Этой характеристике соответствует структурная схема ЦФ 5-го порядка следующего вида (прямая форма I):
T – элемент задержки на один период дискретизации. При реализации на вычислительных устройствах работа фильтра реализуется следующим выражением:
y = a0*x+a1*x1+a2*x2+a3*x3+a4*x4+a5*x5 - (b1*y1+b2*y2+b3*y3+b4*y4+b5*y5)
Здесь a0 соответствует a0 и т.д. Обозначение x1 соответствует задержки x на 1 период дискретизации, x2 - на 2 периода и т.д. Для y1,y2… аналогично. Звёздочка * означает умножение.
Задача расчёта цифрового фильтра заключается в следующих переходах:
s à z, Ak à ak, Bk à bk , для k=0..n, где n- порядок фильтра, в данном случае n=5.
Наиболее распространённым методом расчёта ЦФ является т.н. «метод билинейного преобразования». При использовании данного метода удаётся максимально приблизить АЧХ ЦФ к АЧХ АФ-прототипа. Основная формула билинейного преобразования выглядит следующим образом [1]:
fs=1/T – частота дискретизации.
Из теории известно, что yмножение в частотной области на z-1 эквивалентно задержки отсчёта на время T во временной области, откуда становиться понятным взаимосвязь приведенных выше выражений для H(z) и y.
Значение коэффициента c непосредственно в билинейной формуле равно c=2/T=2fs. Однако при этом АЧХ ЦФ и АЧХ АФ заметно «разбегаются» с увеличением частоты. Поэтому с целью коррекции стали применять его в следующих вариантах [2]:
Мы определились с заменой s à z. Теперь переходим к преобразованию коэффициентов:
Ak à ak, Bk à bk
Расчеты удобно проводить на Mathcad.
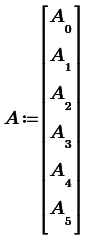
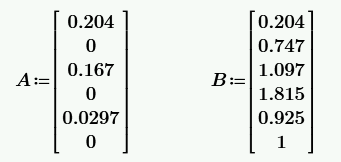
1. Скорректированные коэффициенты аналогового ФНЧ записываем в векторном виде:
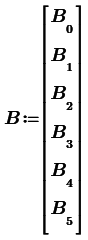
Коэффициенты цифрового фильтра определим с помощью матричных вычислений [2]:
a = P*A b = P*B
Результатом расчета будут векторы коэффициентов цифрового фильтра:
P- матрица Паскаля, которая зависит только от порядка фильтра. Для n=5 она будет иметь вид:
В качестве конкретного примера рассмотрим ФНЧ 5-го порядка со срезом на частоте fc = 200 Гц при частоте дискретизации fs = 2000 Гц. Выбор аналогового фильтра-прототипа рассматривать не будем, поскольку этому вопросу посвящена обширная литература. Предположим, что наc устроил эллиптический фильтр 5-го порядка, который имеет следующую передаточную характеристику [3]:
Запишем его коэффициенты в векторном виде
После вышеупомянутых матричных вычислений получим следующие коэффициенты цифрового фильтра:
Пронормируем все коэффициенты относительно b0 с той целью, чтобы в итоге получить b0=1. Это необходимо для последующей реализации фильтра в виде прямой формы. Окончательно имеем.
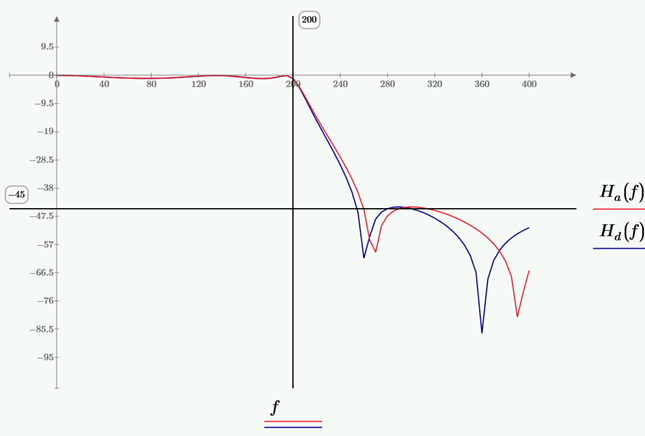
Вычисленные на Mathcad АЧХ аналогового Ha(f) и цифрового Hd(f) фильтров показаны на следующем графике:
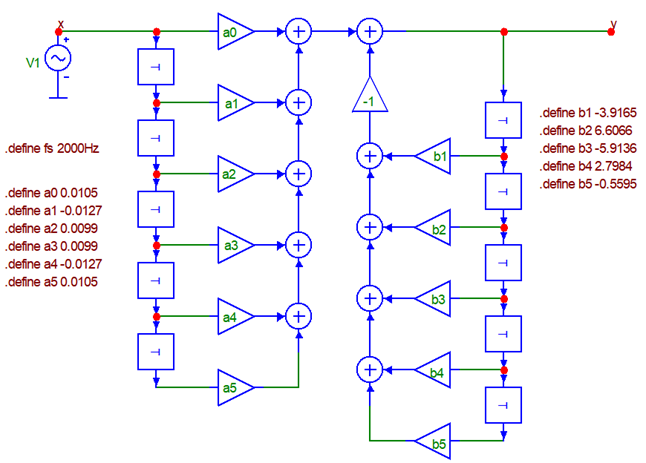
Как следует из графиков аналоговая и цифровая характеристики почти идеально совпадают в полосе пропускания и заметно отличаются за её пределами. Если выбрать частоту дискретизации на порядок выше: 20000 Гц, то расхождение будет практически незаметным. Впрочем, в данном случае, расхождение идет на пользу, т.к. АЧХ цифрового фильтра идёт ещё круче, чем аналогового. Для того, чтобы окончательно убедиться в правильности рассмотренного подхода и корректности приведенных здесь расчётов на MicroСap-12 была построена цифровая модель фильтра, изображённая на следующем рисунке:
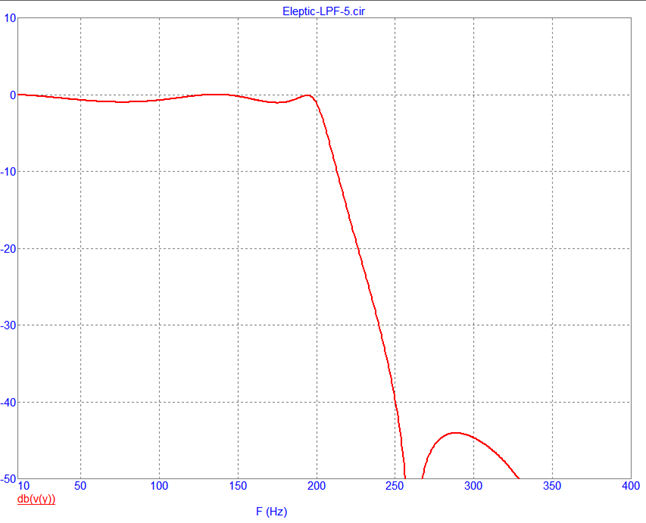
Частота дискретизации и коэффициенты фильтра заданы директивами .define. Ниже показана АЧХ фильтра, полученная в результате моделирования:
Видим, что она соответствует ожидаемой.
Mathcad-программа расчета данного фильтра доступна здесь . Программу нетрудно модифицировать для фильтра любого порядка. Литература и ссылки
2. Phuoc Si Nguyen. Bilinear z-transformation and Pascal’s triangle. 3. Расчет аналогового нормированного эллиптического фильтра нижних частот. |
||||||||
|
|