На главную     ↑ Выше

Цифровой фильтр без операций умножения

Одна из проблем реализации цифровых фильтров заключается в необходимости применения операций умножения, которые отсутствуют в недорогих микроконтроллерах. Однако в ряде случаев удаётся избежать операций умножения, заменив их операциями арифметического сдвига двоичного числа и сложения (вычитания). Например, коэффициент умножения 0.875 в выражении y = x*0.875 можно реализовать как

y = x – x/8

или в записи с арифметическим сдвигом:

y = x - (x>>3).

Запись x>>n означает арифметический сдвиг двоичного числа вправо на n разрядов. Эта операция эквивалентна делению числа на 2^n (два в степени n):

x>>n = x / (2^n)

Запись x<<n означает арифметический сдвиг двоичного числа влево на n разрядов. Эта операция эквивалентна умножению числа на 2^n :

x<<n = x * (2^n)

Рассмотрим многокаскадный рекурсивный цифровой фильтр нижних частот, в котором операции умножения отсутствуют.

Один каскад данного фильтра строится на двух звеньях первого и второго порядков. Звено первого порядка реализуется следующим фрагментом кода:

y = x>>2 + y1 – y1>>2
y1 =y

Или в обычной математической записи:

y = x*0.25 + y1 *0.75
y1 = y

Звено второго порядка реализуется следующим фрагментом кода:

u = y>>4 + ((u1<<1) – (u1>>2)) – (u2 – (u2>>3) – (u2>>4))
u2 =u1
u1 = u

Или в обычной математической записи:

u = y*0.0625 + u1*1.75 – u2*0.8125
u2 =u1
u1 = u

Таким образом мы заменили операции умножения сочетанием операций арифметических сдвигов и сложения (вычитания).

Структурная схема одного (базового) каскада такого фильтра выглядит следующим образом:



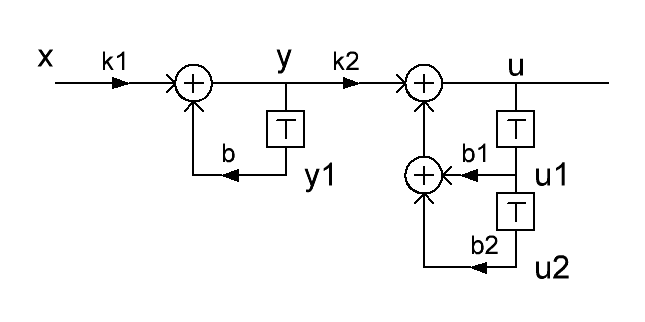Где k1 = 0.25, b = 0.75, k2 = 0.0625, b1 = 1.75, b2 = - 0.8125,
Т – элемент задержки на один период дискретизации.

Многокаскадный фильтр образуется последовательным соединением этого базового каскада.

Программа для вычисления АЧХ на калькуляторе выглядит следующим образом.


;многокаскадный цифровой фильтр без операций умножения
;каждый каскад состоит их двух звеньев первого и второго порядков
b = 1 - 1/4 = 0.75 ; коэффициент b первого звена
k1 = 1/4 ; нормировочный множитель первого звена
b1 = 2 - 1/4 = 1.75 ; коэффициент b1 второго звена
b2 = - (1 - 1/8 - 1/16) = -0.8125 ; коэффициент b2 второго звена
k2 = 1/16 ; нормировочный множитель второго звена
;цикл расчета АЧХ цифрового фильтра
[w = 0:1,0.01 ; цифровая частота
z = cos(w)#-sin(w) ; комплексная переменная z в минус первой степени
H1 = k1/(1 - b*z) ; передаточная функция первого звена
H2 =k2/(1 - b1*z - b2*z^2) ; передаточная функция второго звена
H = H1*H2 ; суммарная передаточная функция двух звеньев (одного каскада)
K1 = modC(H) ; АЧХ первого каскада (модуль суммарной передаточной функции)
K1_db = 20*lg(K1) ; АЧХ однокаскадного фильтра в децибелах
K2_db = 2*K1_db ; АЧХ двухкаскадного фильтра в децибелах
K3_db = 3*K1_db; АЧХ трехкаскадного фильтра в децибелах
val (w, K1_db, K2_db, K3_db); вывод данных в таблицу и на график
]
grafY(-90,10) ; задание пределов по оси Y



Копируя данную программу в текстовое окно калькулятора, получим следующие графики



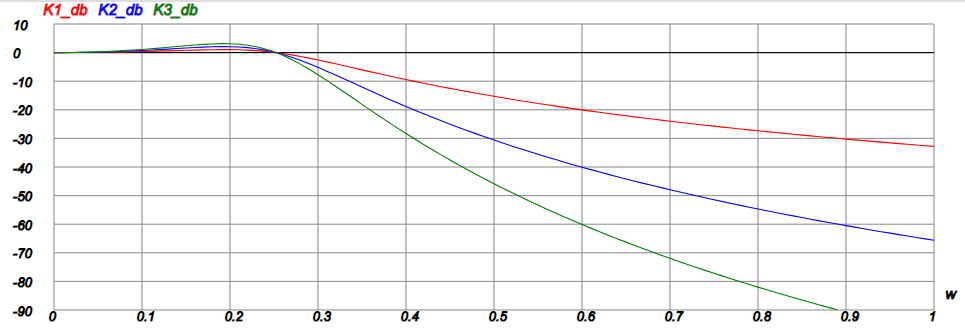Где K1_db, K2_db, K3_db – АЧХ одно-, двух- и трёхкаскадного фильтра соответственно.
АЧХ имеет небольшой подъем в полосе пропускания достигающего значений 1 дБ, 2 дБ и 3 дБ в зависимости от числа каскадов.

По оси абсцисс отложены значения цифровой частоты ω, которая связана с обычной частотой f и частотой дискретизации fd следующим образом:

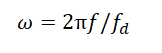Цифровая частота среза данного цифрового ФНЧ равна приблизительно ωc = 0.25.

Для пересчета в обычную частоту воспользуемся формулой:


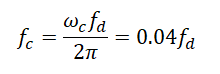Т.е. частота среза фактически определяется частотой дискретизации, изменяя которую можно получать необходимые частоты среза.
  Обратная связь: 
alexander.nekhaev53@gmail.com 		  Поддержать проект   Заказать расчет