| На главную ↑ Выше |
Спектральный анализ. Дискретное преобразование Фурье |
В радиотехнике помимо временнОй функции s(t), называемой процессом или сигналом, принято рассматривать также и её частотный спектр S(f), дающий представление о распределении энергии сигнала по частоте. Для простых сигналов спектр легко находится аналитически [1]. Однако для сложных и составных сигналов приходится прибегать к численным методам. Основным методом вычисления спектра является метод Дискретного преобразования Фурье (ДПФ)[2].
Прежде чем описывать сам метод, отметим важное из теории положение [1], что огибающие спектра для одиночных и периодически повторяющихся импульсов совпадают. Поясним это рисунками.
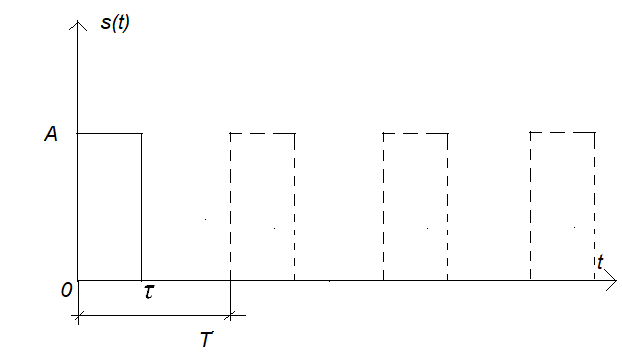
Рис. 1
На рис. 1 показан случай для непериодического (сплошной импульс) и периодического сигнала с периодом Т.
Для первого случая спектр будет сплошным:
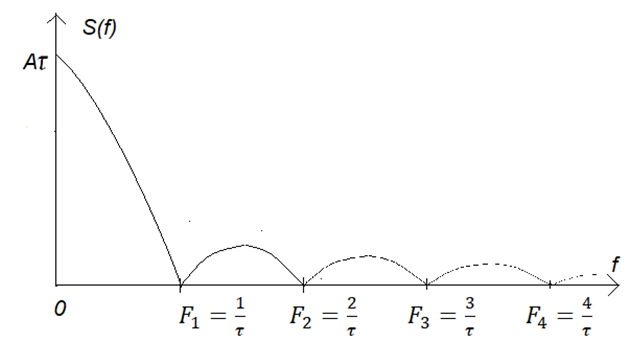
Рис. 2
Для второго - линейчатым, но с точно такой же огибающей:
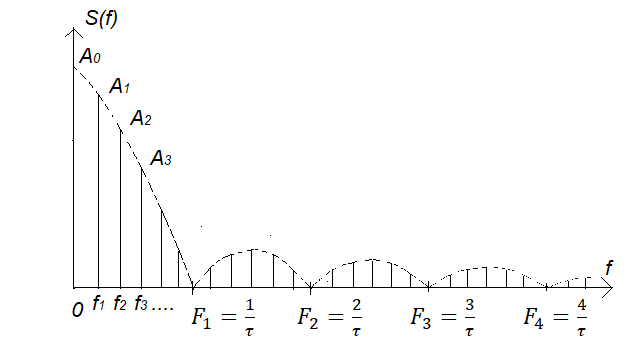
Рис. 3
Здесь f1 = 1/T, f2 = 2f1, f3 = 3f1, … - частоты «гармоник» сигнала, т.е. синусоид, которые в сумме дадут исходный сигнал. Это свойство даёт основание при использовании численных методов не делать принципиального различия между периодическими и непериодическими сигналами. Иными словами, мы всегда можем рассматривать сигнал как периодический, а результаты представлять либо в виде сплошного, либо линейчатого спектра. Такой подход применяется и в калькуляторе КАН. Кроме того, мы можем рассматривать сигнал не в виде непрерывной функции времени s(t), а в виде отчётов sn = s(tn) в дискретные моменты времени tn = nTd, где Td – период дискретизации, n = 0, 1, 2 … N-1 – номера отсчётов.
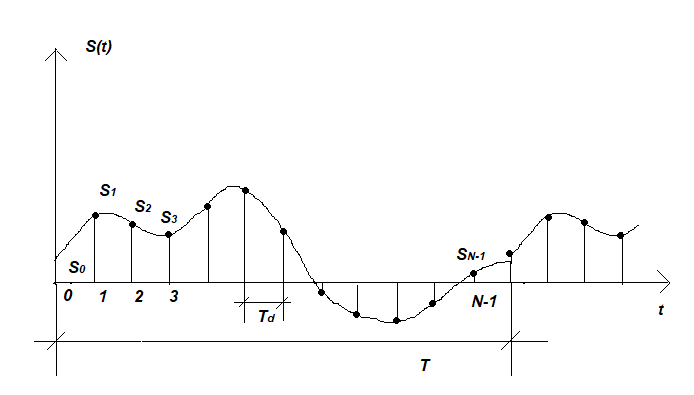
Рис. 4
Оговоримся, что это возможно при одном условии:
Спектр непрерывного сигнала s(t) ограничен верхней частотой ½ fd, где fd = 1/Td – частота дискретизации.
Это условие Теоремы Котельникова [1]. При его соблюдении непрерывный сигнал может быть восстановлен без потерь. Это не выглядит очевидным. Однако вспомним из элементарной геометрии, что для однозначного задания прямой достаточно двух точек, для параболы – трех и, в общем случае, для задания кривой n-го порядка, достаточно n+1-й точки. Теорема Котельникова в некотором смысле является обобщением этого свойства на сигнал бесконечной длины. Это обязательное условие для представления непрерывного сигнала в дискретном (цифровом) виде и следует стремиться к тому, чтобы оно было выполнено.
Итак, мы будем опираться на два положения:
1. Всегда считаем, что сигнал периодический
2. Сигнал представляем в виде отсчётов, следующих с частотой дискретизации.
В этом случае для вычисления составляющих спектра применяется Дискретное преобразование Фурье (ДПФ) [2].
Запишем его в окончательном, удобном для практического применения виде:
Амплитудный спектр
Для k = 0 (постоянная составляющая = значение спектра на нулевой частоте):
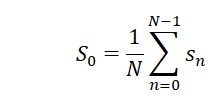
Для k = 1,2,…,N/2:
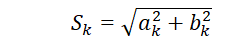
где
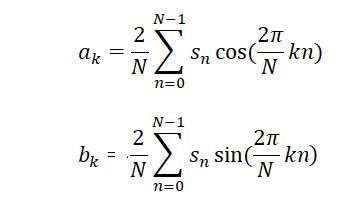
Фазовый спектр
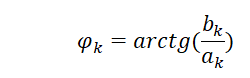
Формулы достаточно простые. Вместе с тем, применение ДПФ требует ясного понимания того, что реально стоит за этими n, k, N. Это необходимо, чтобы избежать грубых ошибок и как можно точнее приблизить результат вычислений к «реальности». В формулах действительные значения для t, f, T заменены на натуральные целые числа: n, k, и N, где n – это номер отчёта по оси времени t, k – это номер отсчёта оси частот f (обычно говорят номер гармоники), N – общее число отсчётов на интервале анализа T.
Для того чтобы убедиться в правильности приведенных выше формул, рассчитаем спектр простейшего синусоидального сигнала:
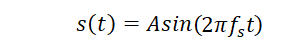
Теоретически, в спектре должна быть всего одна «палка» (гармоника) на частоте fs с амплитудой А. Примем период наблюдения (анализа) T равным периоду синусоиды: T = Ts = 1/fs. В натуральных числах этому соответствует N = Ns = Ts/Td
.
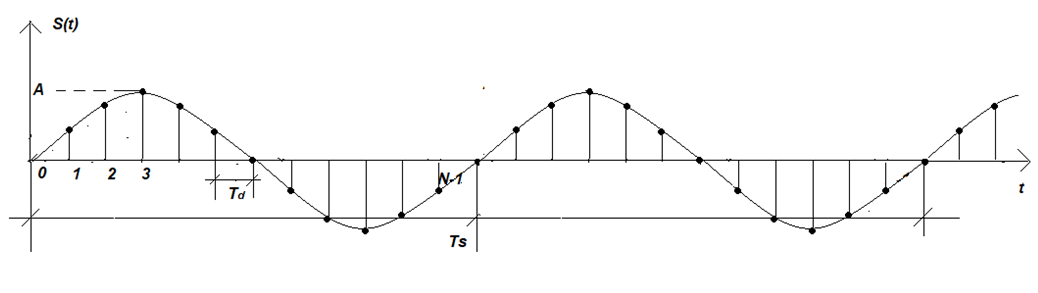
Рис. 5
На рис. 5 изображена синусоида с периодом Ts. Необходимо подчеркнуть, что при рассмотрении периодического сигнала, период наблюдения должен быть равен или кратен периоду самого сигнала. В противном случае, как будет показано, при вычислении «вылезут» нежелательные гармоники Sk, которых на самом деле нет.
Программа для вычисления спектра приведена ниже в Приложении (Программа 1). Её можно скопировать в окно калькулятора КАН и самостоятельно выполнить вычисления (и применять в дальнейшем, подставляя вместо синуса другие сигналы).
В результате вычислений при A=1 мы получим таблицу:
стр. k Sk 1 0 2.88658E-16 2 1 1 3 2 7.39799E-16 4 3 9.93277E-16 5 4 9.78320E-16 6 5 1.38901E-15 ....Как видим Sk = 1 при k = 1и близко к 0 для остальных k (однако не равно точно 0 вследствие погрешности вычислений). То же самое, хотя и не очень наглядно, иллюстрирует следующий график:
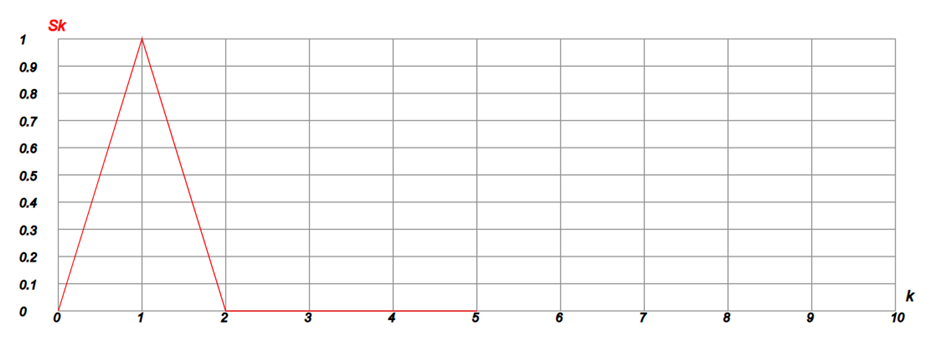
Рис. 6
Что касается графического представления, то в первом графическом окне КАН показывает не отдельные точки или линии (отсчёты), а отрезки, которые соединяют соседние значения. Так сделано потому, что первое графическое предназначено, главным образом, для изображения сигналов как функции времени. Добавим, однако, что в КАН присутствует встроенный анализатор спектра, также основанный на ДПФ. Для изображения спектра функции из первого графического окна используется второе графическое окно, которое открывается при помощи кнопки «Показать». Но пользоваться им имеет смысл в том случае, если ваша программа формирует сигнал как функцию времени. Составим для пояснения простую программу формирования синуса во времени (Приложение. Программа 2). Причём синус возьмём тот же самый, что и в предыдущем примере.
Ниже показан скан с монитора, иллюстрирующий временнУю функцию sn и спектр сигнала Sk. Обратите внимание, что в самом низу установлена опция Спектр линейчатый. И мы получили линию при k = 1 (1000 Гц). Если бы была установлена опция Спектр сплошной, то получили картину как на рис.6.
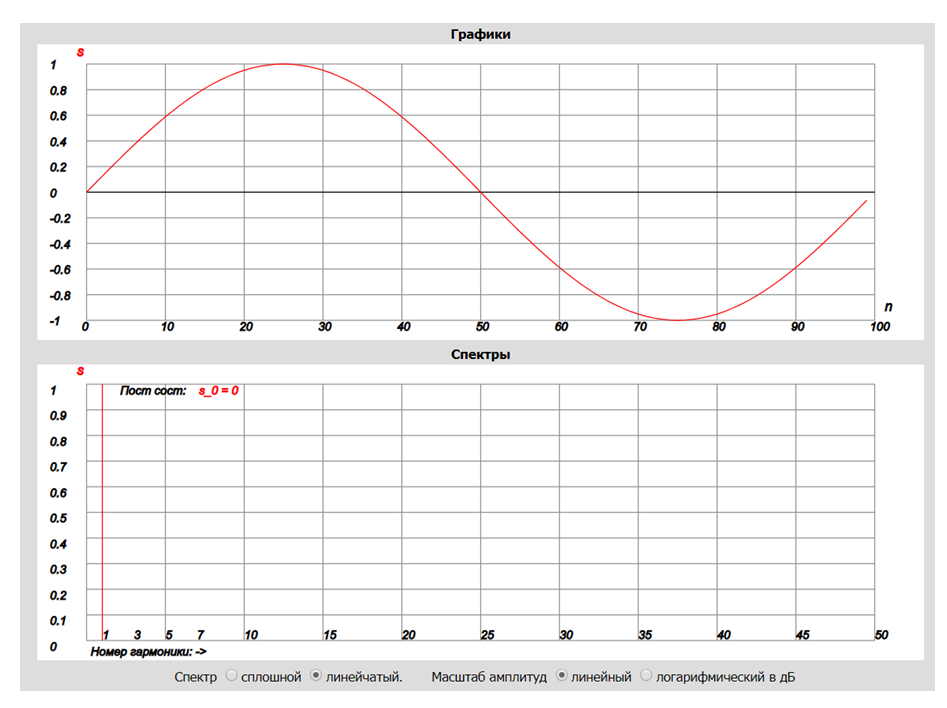
Рис. 7
В дальнейшем будем использовать встроенный анализатор, т.к. программа вычисления ДПФ нам известна (Программа 1), а в калькуляторе КАН она аналогичная.
А что будет, если мы примем период наблюдения равным 10Ts? Для этого в Программе 2 изменим одну строку:
N = 10*Ns ; период наблюденияПолучим следующие графики для сигнала и спектра.
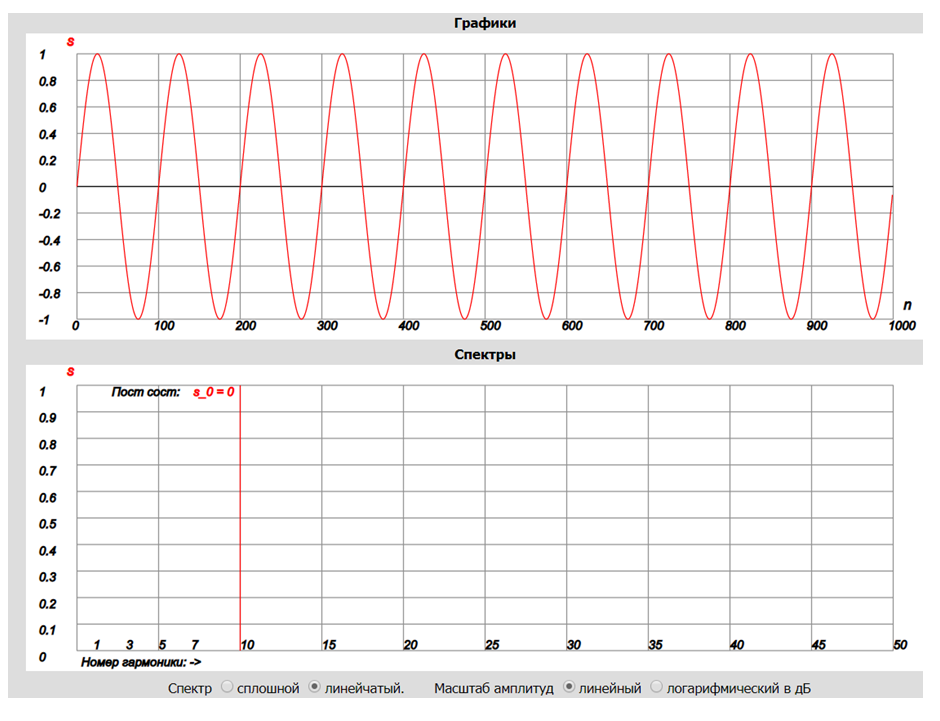
Рис. 8
Как видим единица (Sk = 1) в спектре переместилась на позицию k = 10. Если бы мы приняли N = 20Ns, то получили бы единицу при k=20. Что это означает? Изменяется частота синуса? Но этого быть не должно: во всех случаях она должна быть равной fs= 1000 Гц. Дело в том, что значение k соответствует номеру гармоники определяемой периодом анализа T (или N в натуральных числах). Первая гармоника (k =1) соответствует частоте f1= 1/T, вторая f2 = 2/T и в общем случае fk = k/T. В первом случае период анализа был выбран T = Ts и, следовательно, f1 = fs=1/Ts =1000 Гц. Т.е. первая гармоника анализа точно равна частоте синуса (1000 Гц в Программе 1). Во втором случае: f1 = 1/10Ts = 100 Гц, а f10 = 10/10Ts = 1000 Гц, т.е. единица оказалась на десятой гармонике анализа, но ей, что важно, как и в первом случае соответствует частота 1000 Гц.
А если мы выберем период анализа произвольным образом, например, T = 1.5Ts (N = 1.5Ns в программе 2)? Тогда получим следующую картину:
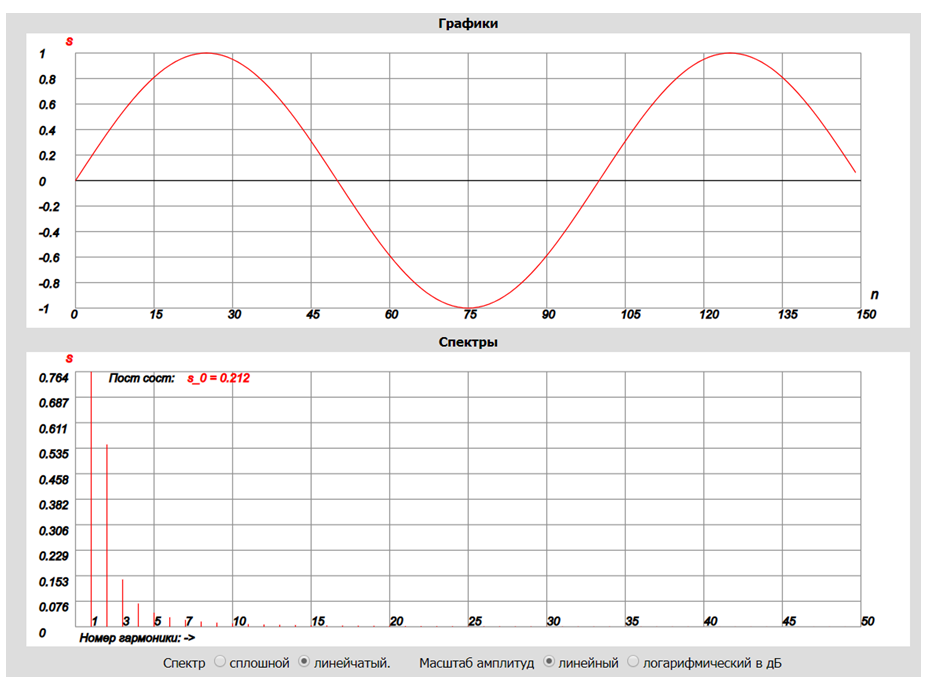
Рис. 9
Как видим, в спектре появились составляющие (в том числе постоянная составляющая), которых теоретически быть не должно. Это означает, что применять ДПФ следует с пониманием физической картины и как-то сопоставлять с теорией. Но теперь мы убедились, что период наблюдения (анализа) должен быть кратен (а лучше просто равен) периоду сигнала (если он периодический) и можем смело применить ДПФ для вычисления спектра более сложного сигнала, теоретический результат для которого нам не известен.
А если сигнал непериодический, например, одиночный импульс? Чтобы осветить этот важный случай, обратимся к рис. 10.
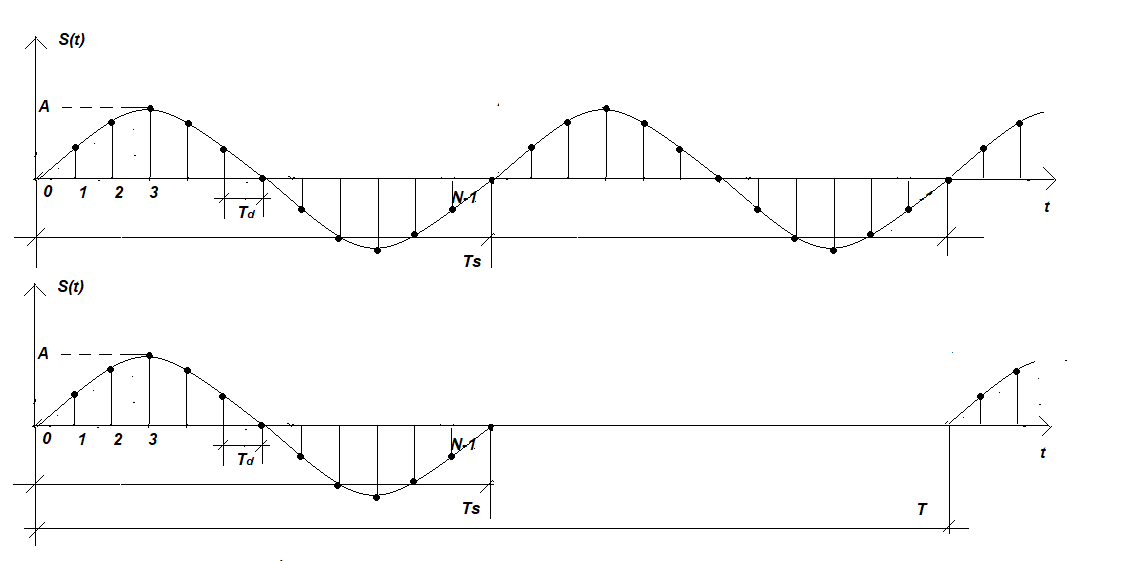
Рис. 10
На первом графике представлен непрерывный периодический синусоидальный сигнал с периодом Ts. В спектре, как мы уже знаем, ему будет соответствовать одна единственная гармоника на частоте fs = 1/Ts и амплитудой А. А как быть, если необходимо узнать спектр одиночного импульса, в частности, с синусоидальным заполнением, да еще и с той же длительностью Ts (или Ns = Ts/Td в натуральных числах)? В этом случае необходимо представить и отразить в программе импульс, как показано на втором графике. Т.е. длительность импульса должна быть Ts < T, а между t = Ts и t = T должны быть нули. Причём, чем больше соотношение T/Ts (или N/Ns), тем лучше. Составим Программу 3 для данного случая и выберем период анализа достаточно большим: T = 10Ts (или N = 10*Ns).
Соответственно и спектр будет иметь иной характер, что мы видим ниже.
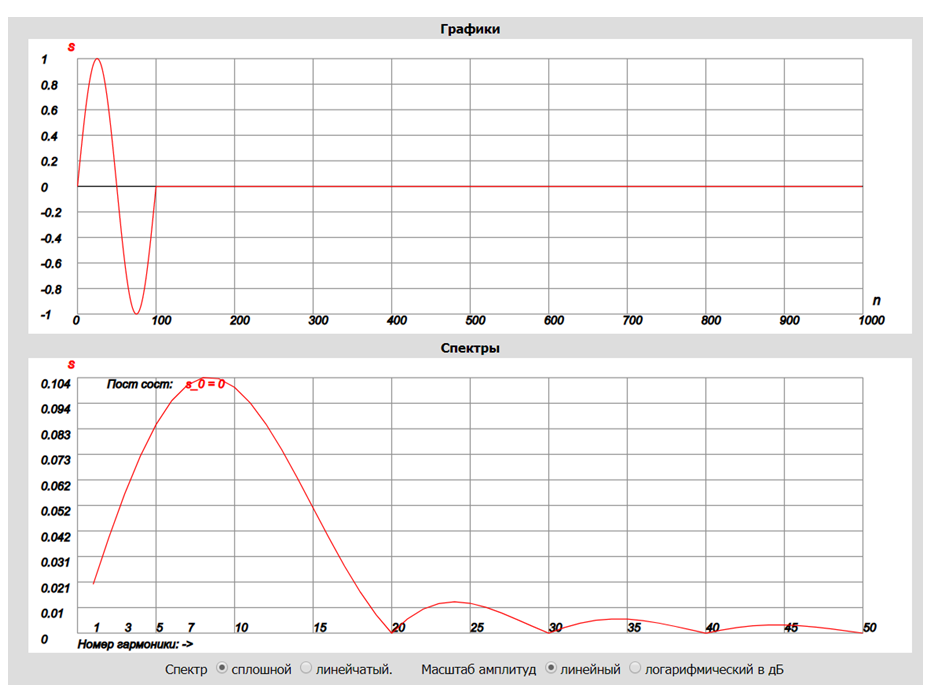
Рис. 11
Обратите внимание, что установлена опция Спектр сплошной, т.к. теперь мы имеем дело с одиночным импульсом и нам важно видеть характер огибающей спектра. Период анализа T в данном случае может быть выбран не кратным Ts. Отметим важный момент: применяя ДПФ, мы всегда имеем дело с периодическими сигналами. На рис. 11 это не показано, но фактически, в данной дискретной математической модели импульс повторяется через каждую 1000 отсчетов. Т.е. импульс повторяется с периодом Т (или N в натуральных числах). Но как мы знаем, огибающая спектра периодической последовательности импульсов совпадает с огибающей спектра одиночного импульса. Поэтому то, что он повторяется на самом деле непринципиально.
При желании, чтобы развеять сомнения, можно воспользоваться интегральным преобразованием Фурье [1] и точно вычислить спектр данного импульса аналитически. Выражение довольно громоздкое и здесь не приводится. Отметим лишь, что имеет место практически идеальное совпадение теоретических значений с вычисленными посредством ДПФ.
В заключение заметим, что спектр, вычисленный с помощью ДПФ, бесконечен и периодичен относительно частоты дискретизации fd. Но на практике нас интересует диапазон значений частот от 0 до fd/2 (в данном примере ей соответствует номер гармоники k = N/2 = 50). Чем меньше значения составляющих спектра при приближении к частоте fd/2, тем точнее результат вычислений будет приближен к теоретическому результату. При рассмотрении непериодических сигналов это достигается путём увеличения соотношения T/Ts (N/Ns), т.е. увеличением интервала анализа по отношению к длительности импульса и выбором достаточно высокой частоты дискретизации fd (число отсчётов в импульсе должно быть достаточно велико, на практике 10 и более). Иными словами, если импульс будет представлен 10-ю и более отчётами, а период наблюдения N=100 или более, то можно говорить о хорошем приближении к теоретически достижимым значениям спектра. Критерием этого, является практически полное затухание составляющих спектра к частоте fd/2, что и является признаком выполнения условия Теоремы Котельникова.
СПИСОК ЛИТЕРАТУРЫ
1. Гоноровский И.С. Радиотехнические цепи и сигналы. «Советское радио», 1971.
2. Отнес Р., Эноксон Л. Прикладной анализ временных рядов. Основные методы. «Мир», 1982.
ПРИЛОЖЕНИЕ
Программа 1
; Дискретное преобразование Фурье (ДПФ)
; спектр синусоидального периодического сигнала.
A = 1 ; амплитуда синуса
fs = 1000 ; частота синуса
fd = 10000 ; частота дискретизации
ws = 2*pi*fs/fd = 0.62832 ; относительная круговая частота синуса
Ns = fd/fs = 10 ; число отсчетов на периоде синуса
N = Ns ; период наблюдения
; цикл вычисления спектра
[k=0:N/2 ; цикл по частоте (номерам гармоник)
{k = 0 ; вычисление постоянной составляющей
Sk = 0
[n=0:N-1 ; цикл по времени
s =A*sin(ws*n) ;сигнал во времени
Sk = Sk + s
]
Sk = Sk/N;
}
{k>0 ; вычисление амплитуд гармоник
a_k = 0
b_k = 0
[n=0:N-1 ; цикл по времени
s = A*sin(ws*n) ;сигнал во времени
x = 2*pi*k/N
a_k = a_k + s*cos(x*n)
b_k = b_k + s*sin(x*n)
]
a_k = a_k*2/N
b_k = b_k*2/N
Sk = sqr(a_k^2 + b_k^2)
}
val(k,Sk); вывод значений в таблицу и на график
]
grafX(0,N)
; спектр синусоидального периодического сигнала.
A = 1 ; амплитуда синуса
fs = 1000 ; частота синуса
fd = 10000 ; частота дискретизации
ws = 2*pi*fs/fd = 0.62832 ; относительная круговая частота синуса
Ns = fd/fs = 10 ; число отсчетов на периоде синуса
N = Ns ; период наблюдения
; цикл вычисления спектра
[k=0:N/2 ; цикл по частоте (номерам гармоник)
{k = 0 ; вычисление постоянной составляющей
Sk = 0
[n=0:N-1 ; цикл по времени
s =A*sin(ws*n) ;сигнал во времени
Sk = Sk + s
]
Sk = Sk/N;
}
{k>0 ; вычисление амплитуд гармоник
a_k = 0
b_k = 0
[n=0:N-1 ; цикл по времени
s = A*sin(ws*n) ;сигнал во времени
x = 2*pi*k/N
a_k = a_k + s*cos(x*n)
b_k = b_k + s*sin(x*n)
]
a_k = a_k*2/N
b_k = b_k*2/N
Sk = sqr(a_k^2 + b_k^2)
}
val(k,Sk); вывод значений в таблицу и на график
]
grafX(0,N)
Программа 2
; Дискретное преобразование Фурье (ДПФ)
; спектр синусоидального периодического сигнала.
A = 1 ; амплитуда синуса
fs = 1000 ; частота синуса
fd = 100000 ; частота дискретизации
ws = 2*pi*fs/fd = 0.06283 ; относительная круговая частота синуса
Ns = fd/fs = 100 ; число отсчетов на периоде синуса
N = Ns ; период наблюдения
; формируем синус
[n = 0:N-1
s = A*sin(ws*n) ; формирование сигнала
val(n,s); вывод значений в таблицу и на график
]
grafX(0,N)
; спектр синусоидального периодического сигнала.
A = 1 ; амплитуда синуса
fs = 1000 ; частота синуса
fd = 100000 ; частота дискретизации
ws = 2*pi*fs/fd = 0.06283 ; относительная круговая частота синуса
Ns = fd/fs = 100 ; число отсчетов на периоде синуса
N = Ns ; период наблюдения
; формируем синус
[n = 0:N-1
s = A*sin(ws*n) ; формирование сигнала
val(n,s); вывод значений в таблицу и на график
]
grafX(0,N)
Программа 3
; Дискретное преобразование Фурье (ДПФ)
; спектр непериодического сигнала.
A = 1 ; амплитуда синуса
fs = 1000 ; частота синуса
fd = 100000 ; частота дискретизации
ws = 2*pi*fs/fd = 0.06283 ; относительная круговая частота синуса
Ns = fd/fs = 100 ; число отсчетов на периоде синуса
N = 10*Ns ; период наблюдения
; формируем синус
[n = 0:N-1
; формирование импульса
{n<Ns s = A*sin(ws*n)}
{n>=Ns s = 0}
val(n,s); вывод значений в таблицу и на график
]
grafX(0,N)
; спектр непериодического сигнала.
A = 1 ; амплитуда синуса
fs = 1000 ; частота синуса
fd = 100000 ; частота дискретизации
ws = 2*pi*fs/fd = 0.06283 ; относительная круговая частота синуса
Ns = fd/fs = 100 ; число отсчетов на периоде синуса
N = 10*Ns ; период наблюдения
; формируем синус
[n = 0:N-1
; формирование импульса
{n<Ns s = A*sin(ws*n)}
{n>=Ns s = 0}
val(n,s); вывод значений в таблицу и на график
]
grafX(0,N)

|
Обратная связь: alexander.nekhaev53@gmail.com |

|
Поддержать проект |

|
Заказать расчет |