| На главную ↑ Выше |
Сглаженные импульсы |
В радиосвязи для передачи информации прямоугольные импульсы практически не используются, поскольку они занимают широкий спектр и, следовательно, требуют широкую полосу частот канала, которая, как правило, ограничена. Для сужения спектра используются сглаженные импульсы.
Для сравнения смоделируем три виды импульсов:
1) Прямоугольный - x
2) Треугольный - y
3) Приподнятый косинус - z
Для этого скопируем в окно калькулятора следующую программу:
; Калькулятор KAN.
t1 = 20
dy = 1/t1
f = 1/(2*0.001*t1) ; частота косинуса
fd = 1000
w = 2*pi*f/fd
y = - dy
; основной цикл
t = 0
[
;прямоугольный импульс
x = 1
{t<10 x = 0}
{t>30 x = 0}
;треугольный импульс
{t<=t1 y = y + dy}
{t>t1 y = y - dy}
{t>=2*t1 y=0}
;приподнятый косинус
z = 1/2*(1 + cos((t - t1)*w))
{t>=2*t1 z=0}
;
val(t,x,y,z)
t = t + 1
{t>100 exit}
]
t1 = 20
dy = 1/t1
f = 1/(2*0.001*t1) ; частота косинуса
fd = 1000
w = 2*pi*f/fd
y = - dy
; основной цикл
t = 0
[
;прямоугольный импульс
x = 1
{t<10 x = 0}
{t>30 x = 0}
;треугольный импульс
{t<=t1 y = y + dy}
{t>t1 y = y - dy}
{t>=2*t1 y=0}
;приподнятый косинус
z = 1/2*(1 + cos((t - t1)*w))
{t>=2*t1 z=0}
;
val(t,x,y,z)
t = t + 1
{t>100 exit}
]
Установим опции спектра «сплошной» и «логарифмический дБ» и нажмем кнопку Вычислить.
Получим следующие графики:
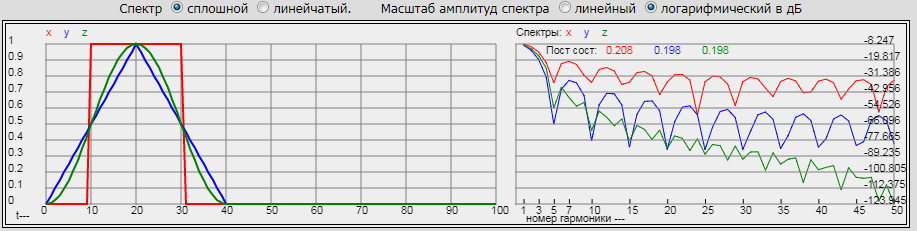 |
На данном графике три импульса и, соответственно, три спектра:
1) Прямоугольный (красный) - x
2) Треугольный (синий) - y
3) Приподнятый косинус (зелёный) – z
В данном случае длительность всех трёх импульсов равна 20 мс (на уровне ½ от амплитуды). Площади всех импульсов так же примерно одинаковы.
На графике спектров видно, что наименее быстро убывает спектр прямоугольного сигнала. Спектр приподнятого косинуса, наоборот, убывает наиболее быстро. Это объясняется тем, что этот импульс самый сглаженный из трёх. Спектр треугольного импульса имеет промежуточные характеристики.

|
Обратная связь: alexander.nekhaev53@gmail.com |

|
Поддержать проект |

|
Заказать расчет |