| На главную ↑ Выше |
Прямоугольный сигнал |
Вторым простейшим сигналом в радиотехнике считается прямоугольный импульс или последовательность прямоугольных импульсов. Не вдаваясь в теорию, рассмотрим чисто практически при помощи компьютерного моделирования, что представляет собой спектр прямоугольного сигнала.
Рассмотрим одиночный импульс длительностью 10 мс. Поскольку при моделировании сигнал представляется дискретными отсчётами, примем длительность одного отсчеты 1 мс. Тогда прямоугольный импульс будет представлен 10-ю отсчетами с номерами 0, 1 … 9. Период наблюдения выберем 100 мс. В текстовое окно калькулятора копируем программу, моделирующую данный сигнал:
; программа моделирования прямоугольного импульса
t1 = 10; длительность импульса в мс
;цикл
t = 0
[
x = 1; значение амплитуды импульса
{t >= t1 x = 0}; переключатель амплитуды импульса в ноль при достижении t1
val(t,x); вывод значений сигнала в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
t1 = 10; длительность импульса в мс
;цикл
t = 0
[
x = 1; значение амплитуды импульса
{t >= t1 x = 0}; переключатель амплитуды импульса в ноль при достижении t1
val(t,x); вывод значений сигнала в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
На рисунке показаны форма импульсного сигнала во времени и его спектр по частоте:
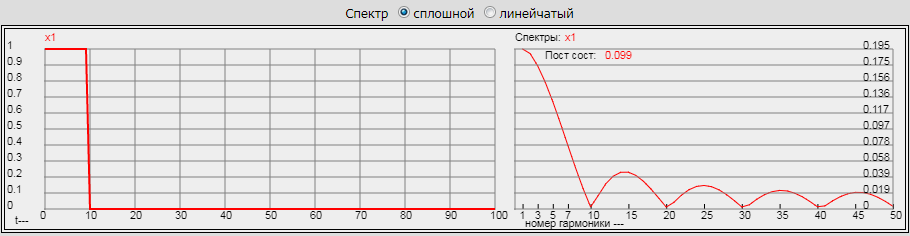 |
Спектр одиночного импульса является сплошным. Частота, соответствующая первой дискретной составляющей спектра, равна 1/0.1 = 10 Гц. (0.1 с = 100 мс – период наблюдения). Частоты, при которых спектр обращается в ноль, равны 100, 200, 300 и т.д. Гц. Они определяются длительностью импульса (в данном случае 10 мс).
Теперь предположим, что мы имеем дело с периодическим импульсным сигналом с периодом 100 мс. Т.е. через каждые 100 мс импульс повторяется. Ничего не меняя в программе, переведем опцию спектра в «линейчатый».
На рисунке в графическом окне увидим спектр периодического сигнала:.
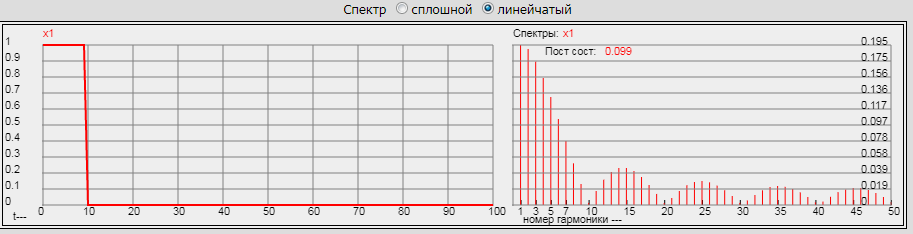 |
Спектр периодического сигнала состоит из дискретных синусоидальных составляющих, называемых гармониками. Первой гармонике соответствуют частота 1/0.1 = 10 Гц – это частота повторения импульсов (на графике мы видим один импульс, который, как мы приняли, повторяется каждые 100 мс). Каждая 10 гармоника (частоты 100, 200, 300 и т.д. Гц) обращается в нуль. Частота 100 Гц соответствуют длительности импульса 1/0.01 (0.01 с = 10 мс). Заметим, что огибающая линейчатого спектра полностью повторяет кривую сплошного спектра одиночного импульса длительностью 10 мс. Эта закономерность справедлива для всех видов импульсного сигнала, не только прямоугольного.
Предполагая, что сигнал периодический, увеличим длительность импульса в 2 раза, задав в программе t1= 20 (20 мс). Получим следующий график:
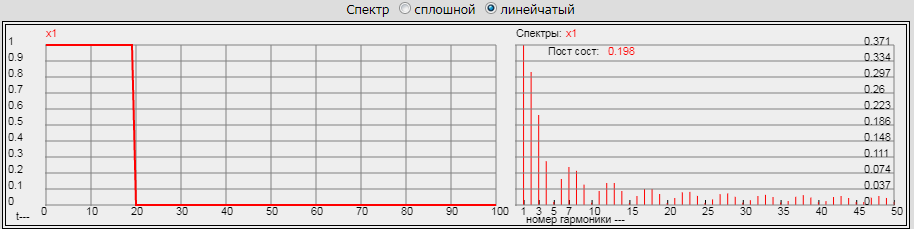 |
Видим, что длительность импульса на графике выросла вдвое, а спектр ровно в 2 раза стал уже. Кроме того, теперь в 0 обращается каждая пятая гармоника, соответствующая частотам 1/0.02 = 50, 100, 150 и т.д. Гц. Эта закономерность (обратная зависимость длительности импульса и ширины спектра) также справедлива для всех видов сигналов. Наконец, рассмотрим оба импульса на одном графике, уменьшив амплитуду второго импульса в 2 раза.
Программа:
; программа моделирования прямоугольного импульса
t1 = 10; длительность первого импульса в мс
t2 = 20; длительность второго импульса в мс
;цикл
t = 0
[
x = 1; значение амплитуды первого импульса
{t >= t1 x = 0}; переключатель амплитуды импульса в ноль при достижении t1
y = 0.5; значение амплитуды второго импульса
{t >= t2 y = 0}; переключатель амплитуды импульса в ноль при достижении t2
val(t,x,y); вывод значений сигнала в таблицу и в графическое окно
t = t + 1
{t=100 exit} ; выход из цикла
]
t1 = 10; длительность первого импульса в мс
t2 = 20; длительность второго импульса в мс
;цикл
t = 0
[
x = 1; значение амплитуды первого импульса
{t >= t1 x = 0}; переключатель амплитуды импульса в ноль при достижении t1
y = 0.5; значение амплитуды второго импульса
{t >= t2 y = 0}; переключатель амплитуды импульса в ноль при достижении t2
val(t,x,y); вывод значений сигнала в таблицу и в графическое окно
t = t + 1
{t=100 exit} ; выход из цикла
]
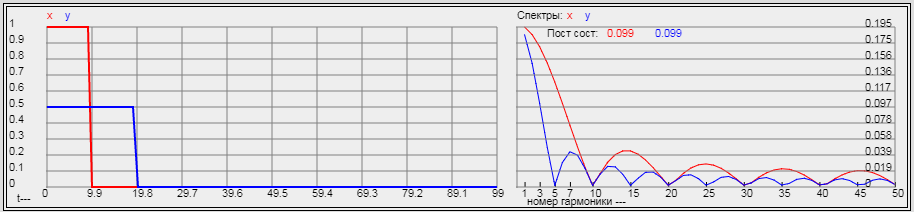 |
На правом графике наглядно видно, что ширина спектра второго импульса уже в 2 раза, чем первого.

|
Обратная связь: alexander.nekhaev53@gmail.com |

|
Поддержать проект |

|
Заказать расчет |