| На главную ↑ Выше |
Синусоидальный сигнал |
Основным видом сигнала в радиотехнике считается синусоидальный сигнал, который часто называют «гармоническим»:
 |
Промоделируем с помощью калькулятора данный вид сигнала с частотой 10 Гц. Поскольку при компьютерном моделировании сигнал представляется в виде дискретных отсчётов, примем интервал времени между отсчетами 0.001 с или 1 мс, что соответствует частоте дискретизации 1000 Гц. Скопируем в текстовое окно калькулятора следующую программу:
; программа моделирования синусоидального сигнала
f = 10 ; частота синусоидального сигнала
fd = 1000 ; частота дискретизации
w = 2*pi*f/fd ; относительная круговая частота
A = 1 ; амплитуда сигнала
; основной цикл
t = 0
[
x = A*sin(w*t) ; синусоидальный сигнал
val(t,x); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
f = 10 ; частота синусоидального сигнала
fd = 1000 ; частота дискретизации
w = 2*pi*f/fd ; относительная круговая частота
A = 1 ; амплитуда сигнала
; основной цикл
t = 0
[
x = A*sin(w*t) ; синусоидальный сигнал
val(t,x); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
Нажмем кнопку «Вычислить» и в графическом окне калькулятора увидим следующие графики:
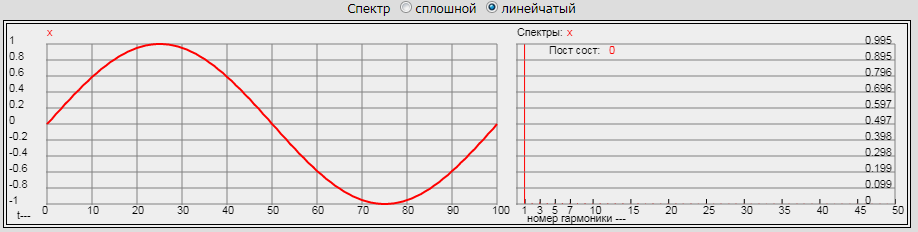 |
Слева график синусоидального сигнала с периодом 100 мс, справа его спектр (опция «Спектр» установлена «линейчатый»). Первая, она же и единственная, гармоника спектра соответствует частоте синусоидального сигнала 1/0.1 = 10 Гц. Таким образом, спектр периодического синусоидального сигнала представлен одной линией, расположенной на частоте этого сигнала. Добавим к этому сигналу еще один «гармонический» сигнал с частотой в 5 раз выше, т.е. f2 = 50 Гц.
Программа будет выглядеть следующим образом:
; программа моделирования синусоидального сигнала
f1 = 10 ; частота синусоидального сигнала 1
f2 = 50 ; частота синусоидального сигнала 2
fd = 1000 ; частота дискретизации
w1 = 2*pi*f1/fd ; относительная круговая частота 1
w2 = 2*pi*f2/fd ; относительная круговая частота 2
A1 = 1 ; амплитуда сигнала 1
A2 = 1 ; амплитуда сигнала 2
; основной цикл
t = 0
[
x1 = A1*sin(w1*t) ; синусоидальный сигнал 1
x2 = A2*sin(w2*t) ; синусоидальный сигнал 2
val(t,x1, x2); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
f1 = 10 ; частота синусоидального сигнала 1
f2 = 50 ; частота синусоидального сигнала 2
fd = 1000 ; частота дискретизации
w1 = 2*pi*f1/fd ; относительная круговая частота 1
w2 = 2*pi*f2/fd ; относительная круговая частота 2
A1 = 1 ; амплитуда сигнала 1
A2 = 1 ; амплитуда сигнала 2
; основной цикл
t = 0
[
x1 = A1*sin(w1*t) ; синусоидальный сигнал 1
x2 = A2*sin(w2*t) ; синусоидальный сигнал 2
val(t,x1, x2); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
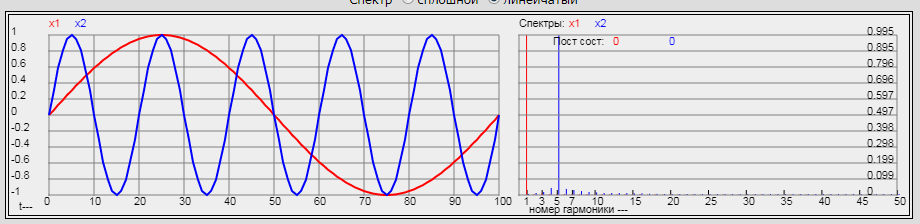
Нажмите кнопку Вычислить. Картина будет такая:
|
Красным цветом обозначен сигнал частотой 10 Гц, синим – сигнал частотой 50 Гц. В спектре имеем две гармоники с частотами 10 и 50 Гц соответственно.
Теперь сложим оба сигнала:
; программа моделирования синусоидального сигнала
f1 = 10 ; частота синусоидального сигнала 1
f2 = 50 ; частота синусоидального сигнала 2
fd = 1000 ; частота дискретизации
w1 = 2*pi*f1/fd ; относительная круговая частота
w2 = 2*pi*f2/fd ; относительная круговая частота
A1 = 1 ; амплитуда сигнала 1
A2 = 1 ; амплитуда сигнала 2
; основной цикл
t = 0
[
x1 = A1*sin(w1*t) ; синусоидальный сигнал 1
x2 = A2*sin(w2*t) ; синусоидальный сигнал 2
x_sum = x1 + x2; сумма двух сигналов
val(t,x_sum); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
f1 = 10 ; частота синусоидального сигнала 1
f2 = 50 ; частота синусоидального сигнала 2
fd = 1000 ; частота дискретизации
w1 = 2*pi*f1/fd ; относительная круговая частота
w2 = 2*pi*f2/fd ; относительная круговая частота
A1 = 1 ; амплитуда сигнала 1
A2 = 1 ; амплитуда сигнала 2
; основной цикл
t = 0
[
x1 = A1*sin(w1*t) ; синусоидальный сигнал 1
x2 = A2*sin(w2*t) ; синусоидальный сигнал 2
x_sum = x1 + x2; сумма двух сигналов
val(t,x_sum); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
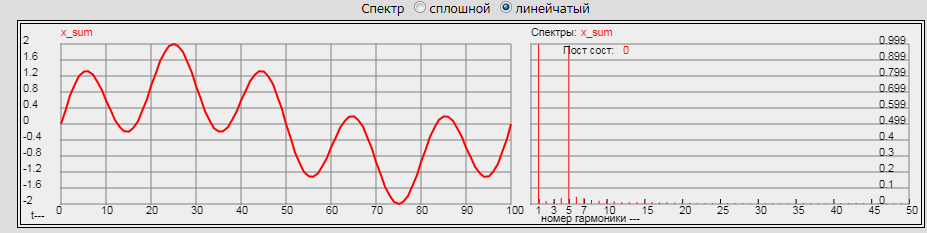
Введя в текстовое окно калькулятора данную программу и, нажав кнопку Вычислить, увидим следующие графики временной формы суммарного сигнала и спектра:
|
Видим, что амплитуда суммарного сигнала выросла в 2 раза, а спектр при этом не изменился.
Заметим, что с помощью суммы синусоидальных сигналов с определёнными амплитудами и фазами можно синтезировать любые виды сигналов, в том числе и прямоугольные.
Чтобы это продемонстрировать используем следующую программу, где суммарный сигнал представлен несколькими нечётными гармониками:
; программа моделирования суммарного сигнала
; частоты гармоник
f1 = 10 ; частота первой гаромоники
fd = 1000 ; частота дискретизации
w1 = 2*pi*f1/fd ; цифровая частота первой гармоники
; амплитуды гармоник
A1 = 1
A3 = 1/3
A5 = 1/5
A7 = 1/7
A9 = 1/9
; основной цикл
t = 0
[
x1 = A1*sin(w1*t); 1-я гармоника
x3 = A3*sin(3*w1*t) ; 3-я гармоника
x5 = A5*sin(5*w1*t) ; 5-я гармоника
x7 = A7*sin(7*w1*t) ; 7-я гармоника
x9 = A9*sin(9*w1*t) ; 9-я гармоника
x_sum = x1 + x3 + x5 + x7 + x9 ; сумма гармоник
val(t,x_sum); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
; частоты гармоник
f1 = 10 ; частота первой гаромоники
fd = 1000 ; частота дискретизации
w1 = 2*pi*f1/fd ; цифровая частота первой гармоники
; амплитуды гармоник
A1 = 1
A3 = 1/3
A5 = 1/5
A7 = 1/7
A9 = 1/9
; основной цикл
t = 0
[
x1 = A1*sin(w1*t); 1-я гармоника
x3 = A3*sin(3*w1*t) ; 3-я гармоника
x5 = A5*sin(5*w1*t) ; 5-я гармоника
x7 = A7*sin(7*w1*t) ; 7-я гармоника
x9 = A9*sin(9*w1*t) ; 9-я гармоника
x_sum = x1 + x3 + x5 + x7 + x9 ; сумма гармоник
val(t,x_sum); вывод значений в таблицу и в графическое окно
t = t + 1
{t>100 exit} ; выход из цикла
]
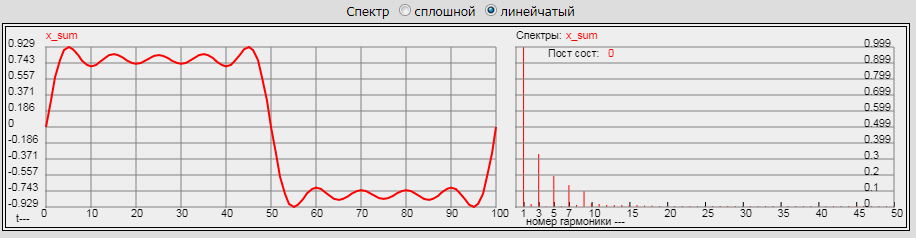
Запустив эту программу, увидим следующий результат:
|
Мы получили почти прямоугольный сигнал. Если количество гармоник увеличивать и дальше по закону, который понятен из текста программы, получим прямоугольный периодический сигнал со скважностью 2, который в радиотехнике принято называть меандром.
Таким образом, из суммы синусоидальных сигналов можно получить любой другой сигнал (синтез), и наоборот, любой сигнал можно представить суммой синусоидальных сигналов (спектральный анализ, преобразование Фурье).

|
Обратная связь: alexander.nekhaev53@gmail.com |

|
Поддержать проект |

|
Заказать расчет |