| На главную ↑ Выше |
Типовые численные методы в инженерной практике.(на примере контрольной работы) |
Численные методы широко применяются в инженерной практике для расчёта практических задач при проектировании различный сооружений и устройств. Инженер, владеющий приёмами численного анализа, способен быстро и легко найти необходимые технические решения в случаях, когда аналитические методы либо невозможны, либо чрезмерно сложны.
Ключевыми словами в данной технологии является слова: «аппроксимация», «интерполяция» и «экстраполяция».
Выполним простые, но во многом типовые вычисления, встречающиеся в инженерной практике. Эти вычисления просто и доступно изложены в методическом пособии [1]. Все расчеты будем проводить на бесплатном и доступном программируемом онлайн-калькуляторе КАН.
Для дальнейших расчётов зададим таблично функцию y(x):
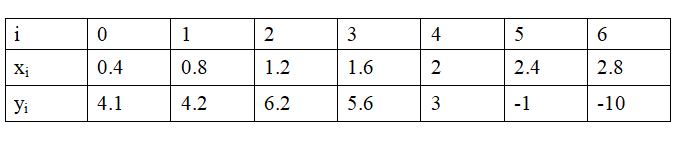
График этой функции имеет вид:
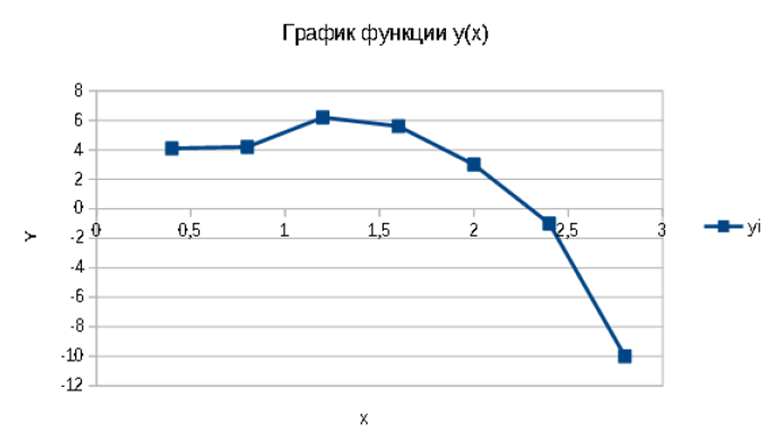
Её можно рассматривать как модель для некоторой физической зависимости, когда известны значения лишь в некоторых точках.
Задача 1. Вычислить значение функции y(x) в точке x_ = 0.49, используя линейную интерполяцию.
Случай не требует особых вычислений, поэтому мы просто приведём решение из [1].
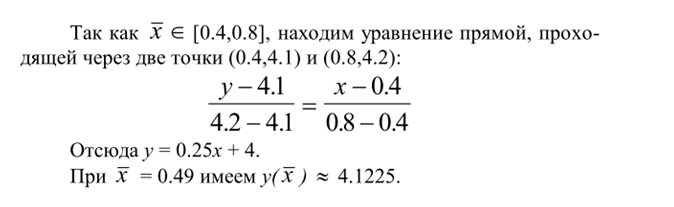
Задача 2. Вычислить значение функции y(x) в точке x_= 0.49, используя квадратичную интерполяцию (интерполяционный многочлен Лагранжа второй степени).

Формула достаточно сложная, поэтому воспользуемся калькулятором КАН.
; Калькулятор KAН.
x = 0.49 ; точка x_
;точка 0
x0 = 0.4
y0 = 4.1
; точка 1
x1 = 0.8
y1 = 4.2
;точка 2
x2 = 1.2
y2 = 6.2
;вычисление по формуле Лагранжа второй степени
L0 = y0*(x - x1)*(x - x2)/((x0 - x1)*(x0 - x2)) = 2.82003
L1 = y1*(x - x0)*(x - x2)/((x1 - x0)*(x1 - x2)) = 1.67737
L2 = y2*(x - x0)*(x - x1)/((x2 - x0)*(x2 - x1)) = -0.54056
L = L0 + L1 + L2 = 3.95684
x = 0.49 ; точка x_
;точка 0
x0 = 0.4
y0 = 4.1
; точка 1
x1 = 0.8
y1 = 4.2
;точка 2
x2 = 1.2
y2 = 6.2
;вычисление по формуле Лагранжа второй степени
L0 = y0*(x - x1)*(x - x2)/((x0 - x1)*(x0 - x2)) = 2.82003
L1 = y1*(x - x0)*(x - x2)/((x1 - x0)*(x1 - x2)) = 1.67737
L2 = y2*(x - x0)*(x - x1)/((x2 - x0)*(x2 - x1)) = -0.54056
L = L0 + L1 + L2 = 3.95684
Отсюда оценка значения функции в точке x_= 0.49:
L(0.49) = L0 + L1 + L2 = 3.95684
Данную программу можно скопировать в окно калькулятора и проверить расчёты. Её также можно использовать для вычисления своих вариантов. Заметим, что полученное значение функции в точке x_ посредством интерполяции 2-го порядка близко к значению полученному выше в Задаче 1. Чем выше порядок интерполяции, тем как правило она точнее.
В данной задаче нам потребовалось три точки. Соответственно, для аппроксимации полиномом Лагранжа n -го порядка, потребуется n+1 точка.
Один из методов аппроксимации – аппроксимация полиномом n-ой степени. Чем больше исходная зависимость отличается от линейной, тем выше должна быть степень полинома. Часто достаточно ограничится небольшим n. Рассмотрим соответствующую задачу.
Задача 3. Для заданной функции y(x) построить аппроксимирующий многочлен третьей степени.

Программа для расчета приведена ниже.
;калькулятор КАН
; декларирование массивов для решения СЛАУ
mas: x[6], y[6], V[4,1], C[4,1], B[4,4], B_1[4,4]
;задаем точки табличной функции
;точка 0
x[0] = 0.4
y[0] = 4.1
; точка 1
x[1] = 0.8
y[1] = 4.2
;точка 2
x[2] = 1.2
y[2] = 6.2
;
;точка 3
x[3] = 1.6
y[3] = 5.6
; точка 4
x[4] = 2
y[4] = 3
;точка 5
x[5] = 2.4
y[5] = -1
;точка 6
x[6] = 2.8
y[6] = -10
;задаём матрицу коэффициентов b (не обязательно)
B = |
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
|
;задаём матрицу (вектор-столбец) коэффициентов c (не обязательно)
C = |0, 0, 0, 0|
;наполняем значениями элементы матрицы B
; с учетом, что индексы матрицы в КАН начинаются с 1
[k =0:3
[l=0:3
B[k+1,l+1] = 0
[i=0:6
B[k+1,l+1] = B[k+1,l+1] + x[i]^(k+l)
]
]
]
;аналогично наполняем значениями элементы вектора-столбца C
[k=0:3
C[k+1,1] = 0
[i=0:6
C[k+1,1] = C[k+1,1] + x[i]^k*y[i]
]
]
;решаем систему линейных уравнений методом обращения матрицы
; вычисляем обратную матрицу
B_1 = revM(B)
; решаем СЛАУ (вычисляем вектор-столбец коэффициентов полинома)
V = |B_1*C|
;собственно коэффициенты
D = V[1,1] = 4.05714
C = V[2,1] = -2.29167
B = V[3,1] = 5.95982
A = V[4,1] = -2.47396
; строим график функции
[х = 0.4:2.8, 0.1
фи = A*х^3 + B*х^2 + C*х + D ; аппроксимирующая функция фи(х)
val(х,фи); вывод таблицы и графика
]
noTab ; запрещаем вывод таблицы
grafY(-10,10) ;задаем пределы по оси Y
grafX(0,4) ; задаем пределы по оси Х
; декларирование массивов для решения СЛАУ
mas: x[6], y[6], V[4,1], C[4,1], B[4,4], B_1[4,4]
;задаем точки табличной функции
;точка 0
x[0] = 0.4
y[0] = 4.1
; точка 1
x[1] = 0.8
y[1] = 4.2
;точка 2
x[2] = 1.2
y[2] = 6.2
;
;точка 3
x[3] = 1.6
y[3] = 5.6
; точка 4
x[4] = 2
y[4] = 3
;точка 5
x[5] = 2.4
y[5] = -1
;точка 6
x[6] = 2.8
y[6] = -10
;задаём матрицу коэффициентов b (не обязательно)
B = |
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
|
;задаём матрицу (вектор-столбец) коэффициентов c (не обязательно)
C = |0, 0, 0, 0|
;наполняем значениями элементы матрицы B
; с учетом, что индексы матрицы в КАН начинаются с 1
[k =0:3
[l=0:3
B[k+1,l+1] = 0
[i=0:6
B[k+1,l+1] = B[k+1,l+1] + x[i]^(k+l)
]
]
]
;аналогично наполняем значениями элементы вектора-столбца C
[k=0:3
C[k+1,1] = 0
[i=0:6
C[k+1,1] = C[k+1,1] + x[i]^k*y[i]
]
]
;решаем систему линейных уравнений методом обращения матрицы
; вычисляем обратную матрицу
B_1 = revM(B)
; решаем СЛАУ (вычисляем вектор-столбец коэффициентов полинома)
V = |B_1*C|
;собственно коэффициенты
D = V[1,1] = 4.05714
C = V[2,1] = -2.29167
B = V[3,1] = 5.95982
A = V[4,1] = -2.47396
; строим график функции
[х = 0.4:2.8, 0.1
фи = A*х^3 + B*х^2 + C*х + D ; аппроксимирующая функция фи(х)
val(х,фи); вывод таблицы и графика
]
noTab ; запрещаем вывод таблицы
grafY(-10,10) ;задаем пределы по оси Y
grafX(0,4) ; задаем пределы по оси Х
График:
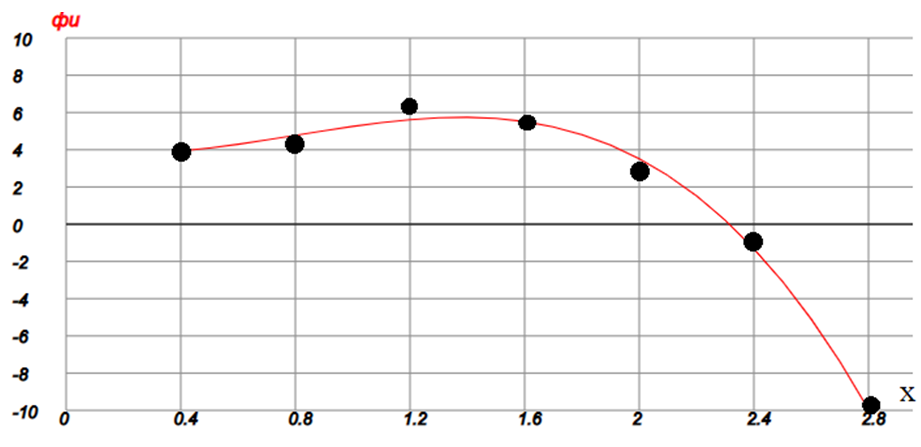
Точками на графике обозначены значения табличной функции y(x).
Задание 4. Вычислить величину определенного интеграла для таблично заданной функции y = y(x) методом трапеций.
В данном методе соседние точки соединяются отрезками прямых линий, образуя трапеции.
Площадь одной трапеции равна:
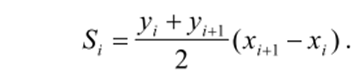
Сумма всех площадей даст оценку определенного интеграла:
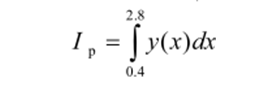
Программа для этой задачи приведена ниже:
;калькулятор КАН
; декларирование массивов для табличной функции
mas: x[6], y[6]
;задаем точки табличной функции
;точка 0
x[0] = 0.4
y[0] = 4.1
; точка 1
x[1] = 0.8
y[1] = 4.2
;точка 2
x[2] = 1.2
y[2] = 6.2
;
;точка 3
x[3] = 1.6
y[3] = 5.6
; точка 4
x[4] = 2
y[4] = 3
;точка 5
x[5] = 2.4
y[5] = -1
;точка 6
x[6] = 2.8
y[6] = -10
;
;вычисляем сумму по методу трапеций
sum = 0
[i=0:5
sum = sum + (y[i] + y[i+1])*(x[i+1] - x[i])/2
]
; выводим значение суммы
val(sum): sum = 6.02
; декларирование массивов для табличной функции
mas: x[6], y[6]
;задаем точки табличной функции
;точка 0
x[0] = 0.4
y[0] = 4.1
; точка 1
x[1] = 0.8
y[1] = 4.2
;точка 2
x[2] = 1.2
y[2] = 6.2
;
;точка 3
x[3] = 1.6
y[3] = 5.6
; точка 4
x[4] = 2
y[4] = 3
;точка 5
x[5] = 2.4
y[5] = -1
;точка 6
x[6] = 2.8
y[6] = -10
;
;вычисляем сумму по методу трапеций
sum = 0
[i=0:5
sum = sum + (y[i] + y[i+1])*(x[i+1] - x[i])/2
]
; выводим значение суммы
val(sum): sum = 6.02
Отсюда Ip ~ 6.02
Задание 5. Найти наибольшее φmax значения для непрерывной на отрезке [x0 ,x6 ]
функции φ(x) методом золотого сечения. Определить точку xmax , в которой это значение достигается.
Опуская теоретическое описание метода золотого сечения (см. в [1]), приведём программу расчета. Суть метода можно также понять из комментариев.
;калькулятор КАН
; нахождение максимума методом золотого сечения
fun: fi = A*x^3 + B*x^2 + C*x + D ; задаем функцию
; задаем значение коэффициентов полинома (определены выше)
A = -2.47396
B = 5.95982
C = -2.29167
D = 4.05714
;значение коэффициентов золотого сечения
k1 = 0.618
k2 = 0.382
; задаем границы начального интервала
a0 = 0.4
b0 = 2.8
;задаем конечный интервал
e_stop = 0.01;
; задаем значение первой итерации
i = 1
; цикл поиска максимума
[
; вычисляем текущий интервал
e = abs(a0 - b0)
; сравниваем текущий интервал с заданным конечным
{e < e_stop exit} ; выходим из цикла если меньше
; вычисляем точки золотого сечения
y = k1*a0 + k2*b0
z = k2*a0 + k1*b0
; вычисляем значения функции в этих точках
x = y
fi_y = fi ; значение fi в точке y
x = z
fi_z = fi ; значение fi в точке z
; сравниваем значения функций и сужаем границы интервала
{fi_y > fi_z b0 = z}
{fi_y <= fi_z a0 = y}
i = i + 1 ; увеличиваем значение итерации
]
fi_max = fi_y
x_max = (a0 + b0)/2
val(i,x_max, fi_max): i = 13, x_max = 1.38355, fi_max = 5.74277
; нахождение максимума методом золотого сечения
fun: fi = A*x^3 + B*x^2 + C*x + D ; задаем функцию
; задаем значение коэффициентов полинома (определены выше)
A = -2.47396
B = 5.95982
C = -2.29167
D = 4.05714
;значение коэффициентов золотого сечения
k1 = 0.618
k2 = 0.382
; задаем границы начального интервала
a0 = 0.4
b0 = 2.8
;задаем конечный интервал
e_stop = 0.01;
; задаем значение первой итерации
i = 1
; цикл поиска максимума
[
; вычисляем текущий интервал
e = abs(a0 - b0)
; сравниваем текущий интервал с заданным конечным
{e < e_stop exit} ; выходим из цикла если меньше
; вычисляем точки золотого сечения
y = k1*a0 + k2*b0
z = k2*a0 + k1*b0
; вычисляем значения функции в этих точках
x = y
fi_y = fi ; значение fi в точке y
x = z
fi_z = fi ; значение fi в точке z
; сравниваем значения функций и сужаем границы интервала
{fi_y > fi_z b0 = z}
{fi_y <= fi_z a0 = y}
i = i + 1 ; увеличиваем значение итерации
]
fi_max = fi_y
x_max = (a0 + b0)/2
val(i,x_max, fi_max): i = 13, x_max = 1.38355, fi_max = 5.74277
Видно, что на 13-й итерации достигнуто конечное значение интервала неопределённости. Максимальное значение функции φ(x) приблизительно равно 5.74277. Сравните с графиком, показанным выше.
Задание 6. Найти один из нулей функции φ(x) (корень уравнения φ(x) = 0) методом бисекции (метод деления отрезка пополам) с точностью <=0.01. Опуская теоретическое описание данного метода (см. в [1]) приведём программу расчета.
Суть метода можно также понять из комментариев.
;калькулятор КАН
; нахождение корня уравнения fi(x) = 0
; методом деления отрезка пополам
fun: fi = A*x^3 + B*x^2 + C*x + D ; задаем функцию
; задаем значение коэффициентов полинома (определены выше)
A = -2.47396
B = 5.95982
C = -2.29167
D = 4.05714
; задаем границы начального интервала
a = 0.4
b = 2.8
;задаем конечный интервал
e_stop = 0.01;
; задаем значение первой итерации
i = 1
; цикл поиска точки пересечения с нулём (корня уравнения fi(x) = 0)
[
; вычисляем текущий интервал
e = abs(a - b)
; сравниваем текущий интервал с заданным конечным
{e < e_stop exit} ; выходим из цикла если меньше
; вычисляем точку на средине интервала
c = (a + b)/2 ;
; вычисляем значения функции в этих точках
x = a
fi_a = fi ; значение fi в точке a
x = b
fi_b = fi ; значение fi в точке b
{fi_a*fi_b >= 0 exit} ; нет пересечения с нулем, выходим из цикла
x = c
fi_c = fi ; значение fi в точке c
{fi_c = 0 exit}; попали точно в ноль, выходим из цикла
; сравниваем значения функций и сужаем границы интервала
{fi_a*fi_c < 0 b = c}; точка пересечения находится на интервале (a,c)
{fi_b*fi_c < 0 a = c}; точка пересечения находится на интервале (c,b)
i = i + 1 ; увеличиваем значение итерации
]
fi_0 = fi_c
x0 = c
val(i,x0, fi_0): i = 9, x0 = 2.32187, fi_0 = -0.10154
; нахождение корня уравнения fi(x) = 0
; методом деления отрезка пополам
fun: fi = A*x^3 + B*x^2 + C*x + D ; задаем функцию
; задаем значение коэффициентов полинома (определены выше)
A = -2.47396
B = 5.95982
C = -2.29167
D = 4.05714
; задаем границы начального интервала
a = 0.4
b = 2.8
;задаем конечный интервал
e_stop = 0.01;
; задаем значение первой итерации
i = 1
; цикл поиска точки пересечения с нулём (корня уравнения fi(x) = 0)
[
; вычисляем текущий интервал
e = abs(a - b)
; сравниваем текущий интервал с заданным конечным
{e < e_stop exit} ; выходим из цикла если меньше
; вычисляем точку на средине интервала
c = (a + b)/2 ;
; вычисляем значения функции в этих точках
x = a
fi_a = fi ; значение fi в точке a
x = b
fi_b = fi ; значение fi в точке b
{fi_a*fi_b >= 0 exit} ; нет пересечения с нулем, выходим из цикла
x = c
fi_c = fi ; значение fi в точке c
{fi_c = 0 exit}; попали точно в ноль, выходим из цикла
; сравниваем значения функций и сужаем границы интервала
{fi_a*fi_c < 0 b = c}; точка пересечения находится на интервале (a,c)
{fi_b*fi_c < 0 a = c}; точка пересечения находится на интервале (c,b)
i = i + 1 ; увеличиваем значение итерации
]
fi_0 = fi_c
x0 = c
val(i,x0, fi_0): i = 9, x0 = 2.32187, fi_0 = -0.10154
Итак корень уравнения φ(x) = 0, полученный на 9-й итерации, приблизительно равен 2.32187. Сравните с графиком, показанным выше.
Библиография
1. ЧИСЛЕННЫЕ МЕТОДЫ. Методические указания и задания к контрольной работе. 4-е издание, переработанное и дополненное. Составители Н.В. Лаходынова, И.А. Иконникова, Г.А. Онопенко. Томский государственный архитектурно-строительный факультет. Томск, 2017.

|
Обратная связь: admin@нехаев.рф |

|
Поддержать проект |