На главную     ↑ Выше

Связанные колебательные контуры
Курсовая работа

    Связанные LC-колебательные контуры широко применяются в радиотехнике, в частности для согласования каскадов радиоприёмных устройств и получения частотной избирательности. Выполним расчёт системы связанных колебательных контуров на примере, изложенном в методическом пособии [1]. Все расчеты будем проводить на программируемом онлайн-калькуляторе КАН.



        

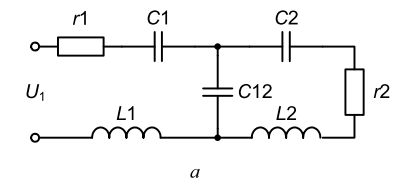
Расчет основных параметров контуров

В методичке [1] это выглядит следующим образом:



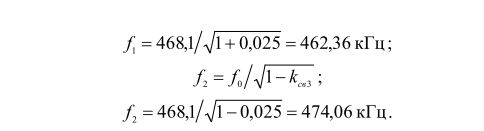
На языке калькулятора КАН аналогичные расчёты проведём, составив следующую программу:

; Калькулятор KAН.
;резонансная частота колебательного контура
L = 290E-6
C = 400E-12
Q = 80
U1m = 11
f0 = 1/(2*pi*sqr(L*C)) = 467295.0031
; Характеристическое сопротивление контуров
ro = sqr(L/C) = 851.46932
; Сопротивление потерь контуров
r = ro/Q = 10.64337
;Критический коэффициент связи первичного контура
k_kr1 = 0.49/Q = 0.00613
;Критический коэффициент связи вторичного контура
k_kr2 = 1/Q = 0.0125
;С учетом выражения А = k_св*Q найдем коэффициенты связи k св
;первичного контура:
A = 0.5
k_sv1 = A*k_kr1 = 0.00306
A = 1
k_sv2 = A*k_kr1 = 0.00613
A = 2
k_sv3 = A*k_kr1 = 0.01225
;вторичного контура:
A = 0.5
k_sv1 = A*k_kr2 = 0.00625
A = 1
k_sv2 = A*k_kr2 = 0.0125
A = 2
k_sv3 = A*k_kr2 = 0.025
;Частоты связи для вторичного контура при k_кр < k_св = k св3
f1 = f0/sqr(1 + k_sv3) = 461561.10492
f2 = f0/sqr(1 - k_sv3) = 473248.04568

Частоты рассчитаны в Гц. Видно что результаты практически совпадают с теми, что приведены в [1]. В КАН вычисления проводятся с очень высокой точностью, ограниченной лишь возможностями Java Script. Скопировав данную программу в окно калькулятора, вы можете произвести расчёты для своего варианта. Вместо цифр, напечатанных полужирным шрифтом, калькулятор подставит новые значения.

Частотные характеристики контуров

Формулы берём из методички [1] .



Расчет проводится для трёх значений A = 0.5, 1, 2. Вместо лицензионного пакета MathCAD используем бесплатный калькулятор КАН.

Программа для расчета:

;калькулятор КАН
;Амплитудно-частотная характеристика тока первичного контура
Q = 80
U1m = 11
r = 10.64337
f0 = 467295.0031
[f = 450000:485000, 500
a = (f/f0 - f0/f)*Q
A = 0.5
I11m = (U1m/r)*sqr(1 + a^2)/sqr((1 - a^2 + A^2)^2 + 4*a^2)
A = 1
I12m = (U1m/r)*sqr(1 + a^2)/sqr((1 - a^2 + A^2)^2 + 4*a^2)
A = 2
I13m = (U1m/r)*sqr(1 + a^2)/sqr((1 - a^2 + A^2)^2 + 4*a^2)
val(f, I11m, I12m, I13m); вывод таблицы данных и графика
]
grafY(0,1) ;Задание пределов по оси Y
 ---------------- Таблица данных ------------
стр. f     I11m   I12m   I13m 
1 450000 0.17001 0.17331 0.18781 
2 450500 0.17509 0.17868 0.19455 
3 451000 0.18047 0.1844 0.20181 
4 451500 0.18618 0.19048 0.20964 
................................
71 485000 0.17237 0.17581 0.19094


График:



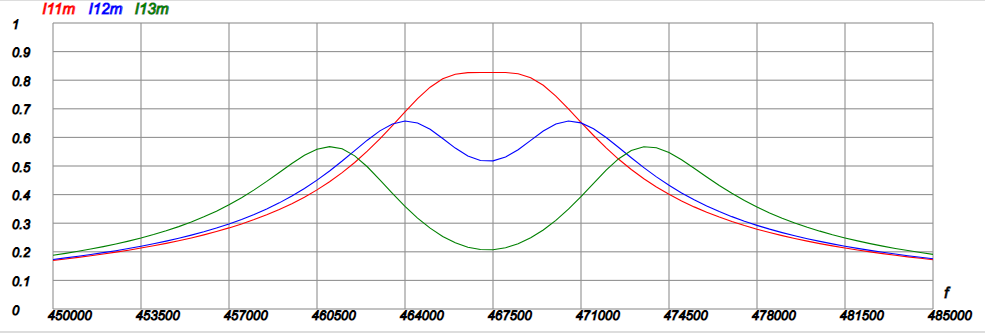
Сравним с графиком, приводимым в [1]:



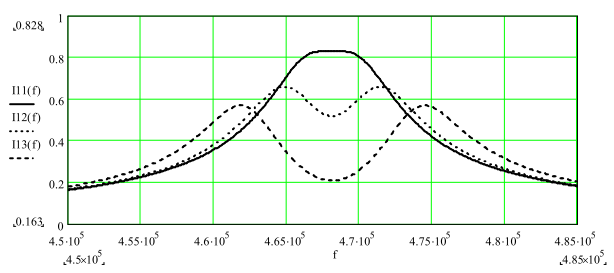
Видно, что результаты идентичны.
Программу нетрудно видоизменить для расчёта АЧХ тока вторичного контура.


Библиография

1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КУРСОВОМУ ПРОЕКТИРОВАНИЮ ПО ДИСЦИПЛИНЕ «ОСНОВЫ ТЕОРИИ ЦЕПЕЙ».
Д.Н. Романов. Муромский институт (филиал) федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых»
  Обратная связь: admin@нехаев.рф   Поддержать проект