
|
Комбинаторика с калькулятором КАН |
В разделе математики, который принято называть комбинаторикой (иногда соединения ), принято различать три типа комбинаций: перестановки, размещения и сочетания. В калькуляторе КАН для вычислений данных комбинаций предусмотрены три встроенные функции. Рассмотрим их по порядку .
Перестановки
Рассмотрим простой пример из справочника с.243: Найти число перестановок из трёх элементов a, b, c. Каким бы образом мы не переставляли эти элементы получим ровно 6 вариантов перестановок. Например:
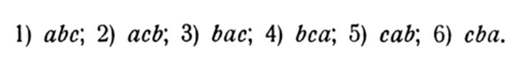
В общем случае для m- элементов справедлива формула:
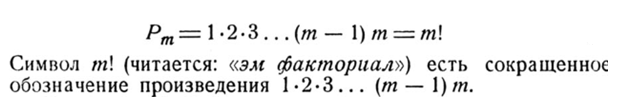
В калькуляторе КАН для вычисления факториала имеется встроенная функция fct(m). Для рассмотренного случая:
fct(3) = 6
Размещения
Пример. Найти число комбинаций из 4-х элементов a, b, c, d по 2. Получим 12 вариантов:
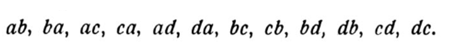
Эти комбинации называются размещениями. Для вычисления числа размещений справедлива формула:
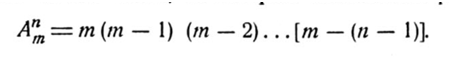
где m<=n.
Для рассмотренного примера n = 2, m = 4.
В калькуляторе КАН для вычисления числа размещений имеется встроенная функция prm(n,m). Для рассмотренного примера:
prm(2,4) = 12
Сочетания
В рассмотренном выше примере учитывался порядок элементов. Например, ab и ba – разные комбинации. Если порядок не учитывать, то получим всего 6 комбинаций:
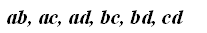
Комбинация такого типа (где порядок не важен) называются сочетаниями. Для определения их числа применяется формула:
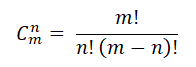
где m<=n.
В калькуляторе КАН для вычисления числа сочетаний имеется встроенная функция cmb(n,m). Для рассмотренного примера:
cmb(2,4) = 6

|
Обратная связь: admin@нехаев.рф |

|
Поддержать проект |