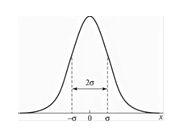
Распределение Гаусса (одномерное)


    Распределение Гаусса или нормальное распределение задаётся формулой:
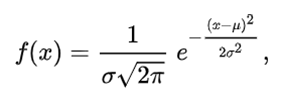
где σ – среднеквадратичное отклонение, μ – математическое ожидание. Такое распределение принято называть дифференциальным или распределением плотности вероятностей. Ниже приведена программа для калькулятора КАН вычисления значений f(x) для трёх значений параметра σ = 0.5, 1, 2 и μ = 0.

;КАН
;дифференциальное распределение по закону Гаусса
;задаём функцию
fun: f = exp(-((x - mo)^2/(2*sigma^2)))/(sigma*sqr(2*pi))
mo = 0 ; математическое ожидание
N = 1000 ; число точек по оси Х
x1 = -5 ; нижний предел по оси Х
x2 = 5 ; верхний предел по оси Х
dx = (x2 - x1)/N ; шаг по оси Х
; цикл вычисления и построения графиков для разных sigma
[x = x1:x2,dx
     sigma = 0.5 ;задаем sigma
     f_05 = f ; вычисляем значение f
     sigma = 1 ;задаем sigma
     f_1 = f ; вычисляем значение f
     sigma = 2 ;задаем sigma
     f_2 = f ; вычисляем значение f
     val(x,f_05, f_1, f_2); вывод значений в таблицу и на график
]
noTab ; запрет вывода таблицы (только графики)
grafX(x1,x2) ; задание пределов графика по оси X



Результатом вычислений будет следующий график дифференциального распределения:



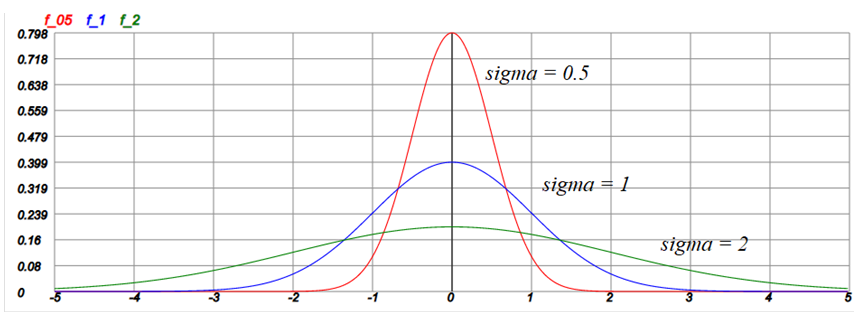
Наряду с дифференциальной формой распределения, применяется также интегральная форма, которая представляет собой интеграл от определённой выше функции f(x):
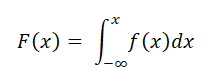
Ниже приведена программа вычисления F(x) для трёх значений параметра σ = 0.5, 1.0, 2.0.

;КАН
;интегральное распределение по закону Гаусса
;задаём функцию
fun: f = exp(-((x - mo)^2/(2*sigma^2)))/(sigma*sqr(2*pi))
mo = 0 ; математическое ожидание
; цикл вычисления и построения графиков для разных sigma
F_05 = 0
F_1 = 0
F_2 = 0
N = 1000 ; число точек по оси Х
x1 = -5 ; нижний предел по оси Х
x2 = 5 ; верхний предел по оси Х
dx = (x2 - x1)/N ; шаг по оси Х
[x = x1:x2, dx
     sigma = 0.5 ;задаем sigma
     F_05 = F_05 + f*dx ; вычисляем значение f
     sigma = 1 ;задаем sigma
     F_1 = F_1 + f*dx ; вычисляем значение f
     sigma = 2 ;задаем sigma
     F_2 = F_2 + f*dx ; вычисляем значение f
     val(x,F_05, F_1, F_2); вывод значений в таблицу и на график
]
noTab ; запрет вывода таблицы (только графики)
grafX(x1,x2) ; задание пределов графика по оси X


Результатом вычислений будет следующий график интегрального распределения:



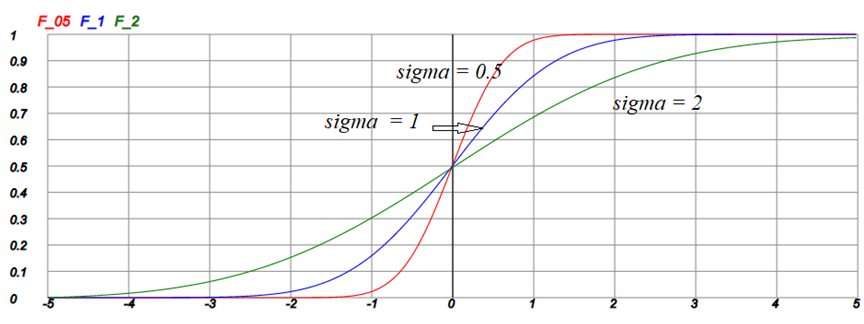
Данные программы могут быть использованы для собственных вычислений.
  Обратная связь: admin@нехаев.рф   Поддержать проект