| На главную ↑ Выше |
Метод контурных токов |
| Заказать расчет |
Элементы теории
Задача анализа линейной электрической цепи (ЛЭЦ) заключается в нахождении токов всех её ветвей, напряжений в узлах и на элементах цепи, в вычислении передаточной функции цепи и других её характеристик. Один из основных методов анализа ЛЭЦ – т.н. метод контурных токов. На следующем рисунке показана электрическая цепь, состоящая из двух источников ЭДС: E1, E2 (в общем случае переменного тока), пяти сопротивлений Z1, … , Z5 (в общем случае комплексных) и трёх контуров k1, k2, k3.
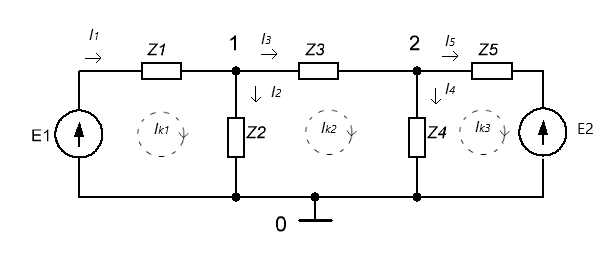 |
| Рис.1 |
Токи (в общем случае комплексные) в ветвях обозначены как I1, I2, I3, I4, I5 . Т.н. контурные токи обозначены как Ik1, Ik2, Ik3. Для данной цепи система уравнений контурных токов, основанная на законах Ома и Кирхгофа, выглядит следующим образом:
| Ik1Z11 - Ik2Z12 - Ik3Z13 = E1 | (1) | ||
| - Ik1Z21 + Ik2Z22 - Ik3Z23 = 0 | (2) | ||
| - Ik1Z31 - Ik2Z32 + Ik3Z33 = - E2 | (3) |
Ik1, Ik2, Ik3 – контурные токи, которые предстоит найти.
Zij – т.н. контурные сопротивления, которые определяются заданными сопротивлениями в ветвях Z1, … , Z5 следующим образом:
1) Т.н. собственные контурные сопротивления:
Z11 = Z1 + Z2, Z22 = Z2 + Z3 + Z4, Z33 = Z4 + Z52) Т.н. общие контурные сопротивления
Z12 = Z21 = Z2, Z23 = Z32 = Z4Таким образом, мы имеем систему из трёх линейных уравнений (1) – (3) с тремя неизвестными Ik1, Ik2, Ik3.
Решив эту систему, т.е. определив контурные токи Ik1, Ik2, Ik3, мы сможем определить токи ветвей для данной цепи:
I1 = Ik1 I2 = Ik1 – Ik2 I3 = Ik2 I4 = Ik2 – Ik3 I5 = Ik3Если у ветви данного контура нет смежного контура, то ток ветви равен контурному току. При наличии смежного контура, ток ветви равен разности контурных токов смежных контуров. При этом слева должен быть контурный ток, который совпадает по направлению с выбранным направлением тока ветви.
Обратим внимание на знаки. В системе уравнений (1) – (3) в левой части все слагаемые с собственными контурными сопротивлениями имеют знак плюс, а все слагаемые с взаимными сопротивлениями имеют знак минус. В правой части ЭДС (а это может быть и сумма ЭДС ветвей данного контура) записывается со знаком плюс если её направление совпадает с выбранным направлением контурного тока, и со знаком минус в противном случае. Направление контурных токов - по часовой, либо против часовой стрелки, вообще говоря, задаётся произвольно. Здесь оно задано по часовой стрелке. Направление токов в ветвях также задаётся произвольно. «Истинное» направление тока будет учтено в ответе в виде знака плюс или минус. Знак минус означает, что «истинное» направление противоположно выбранному.
При необходимости можно вычислить так же и напряжения Um на сопротивлениях ветвей Zm:
Um = Im Zm
В матричной форме система уравнений (1) – (3) записывается следующим образом:
E = Z•I (4)
где
E – вектор-столбец из элементов E1,0, -E2, (в общем случае, элемент вектора Ek это сумма всех ЭДС по k-му контуру с учётом знака),
I – вектор-столбец из элементов Ik1, Ik2, Ik3,
Z – матрица контурных сопротивлений из элементов Zij, причем при i ≠ j перед Zij ставится минус:
В общем случае для системы из n-контуров:
| Z = |
|
Решение уравнения (4) имеет вид:
I = Z-1•E (5)
где Z-1 – матрица, обратная матрице Z.
Данные рассуждения нетрудно обобщить на схему, состоящую из произвольного количества контуров. В любом случае составляется уравнение (4) и находится его решение (5). Ниже мы рассмотрим две практические задачи и покажем как можно найти решение, используя возможности калькулятора KAN .
Практическая задача на постоянном токе
Рассмотрим следующую задачу . Ниже представлена схема из трёх контуров: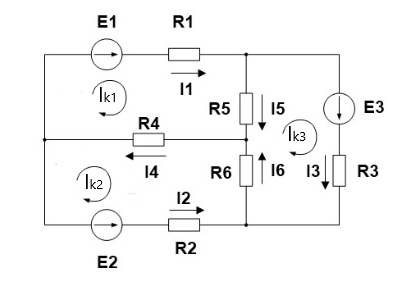 |
| Рис.2 |
Дано:
1) значения ЭДС источников (контурные ЭДС):
E1 = 80 В
E2 = 50 В
E3 = 60 В
2) значения сопротивлений:
R1 = 10 Ом
R2 = 15 Ом
R3 = 20 Ом
R4 = 25 Ом
R5 = 30 Ом
R6 = 35 Ом
Составим текст программы для данной задачи:
; Калькулятор KAN. http://калькулятор.нехаев.рф/calc/calculator.html
; Метод контурных токов. Постоянный ток
;задача - https://electroandi.ru/toe/metod/metod-konturnykh-tokov-reshenie-zadach.html
mas: Z[3,3], Zrev[3,3], E[3,1], I[3,1] ; декларирование массивов для элементов матриц
;--------------------- ДАНО: --------------------------------
; значения ЭДС источников (контурные ЭДС)
E1 = 80
E2 = 50
E3 = 60
; значения сопротивлений
R1 = 10
R2 = 15
R3 = 20
R4 = 25
R5 = 30
R6 = 35
;------------------------- РАСЧЁТ -------------------------------
format(dec,5) ; формат выводимых чисел
; значение контурных сопротивлений
Z11 = R1 + R4 + R5 = 65
Z12 = R4 = 25
Z13 = R5 = 30
Z21 = Z12 = 25
Z22 = R2 + R4 + R6 = 75
Z23 = R6 = 35
Z31 = Z13 = 30
Z32 = Z23 = 35
Z33 = R3+ R5 + R6 = 85
; матрица контурных сопротивлений
Z = |
Z11 -Z12 -Z13
-Z21 Z22 -Z23
-Z31 -Z32 Z33
|
; значения контурных ЭДС источников
Ek1 = E1 = 80
Ek2 = - E2 = -50
Ek3 = E3 = 60
; матрица ЭДС источников (контурных ЭДС)
E = |
Ek1
Ek2
Ek3
|
Zrev = revM(Z) ; вычисление реверсивной матрицы контурных сопротивлений
I = |Zrev*E| ; вычисление контурных токов (решение системы уравнений)
; вывод значений контурных токов
valM(I) : I = |2.72699, 1.26373, 2.18871|
; расчет значений токов ветвей
I1 = I[1,1] = 2.72699
I2 = - I[2,1] = -1.26373
I3 = I[3,1] = 2.18871
I4 = I[1,1] - I[2,1] = 1.46326
I5 = I[1,1] - I[3,1] = 0.53828
I6 = -I[2,1] + I[3,1] = 0.92498
;
;------------ ПРОВЕРКА РАСЧЁТА ---------------
;----------- ЭНЕРГОБАЛАНС -------------
Pe = E1*I1 + E2*I2 + E3*I3 = 286.29544
Pi = I1^2*R1 + I2^2*R2 + I3^2*R3 + I4^2*R4 + I5^2*R5 + I6^2*R6 = 286.29544
; Метод контурных токов. Постоянный ток
;задача - https://electroandi.ru/toe/metod/metod-konturnykh-tokov-reshenie-zadach.html
mas: Z[3,3], Zrev[3,3], E[3,1], I[3,1] ; декларирование массивов для элементов матриц
;--------------------- ДАНО: --------------------------------
; значения ЭДС источников (контурные ЭДС)
E1 = 80
E2 = 50
E3 = 60
; значения сопротивлений
R1 = 10
R2 = 15
R3 = 20
R4 = 25
R5 = 30
R6 = 35
;------------------------- РАСЧЁТ -------------------------------
format(dec,5) ; формат выводимых чисел
; значение контурных сопротивлений
Z11 = R1 + R4 + R5 = 65
Z12 = R4 = 25
Z13 = R5 = 30
Z21 = Z12 = 25
Z22 = R2 + R4 + R6 = 75
Z23 = R6 = 35
Z31 = Z13 = 30
Z32 = Z23 = 35
Z33 = R3+ R5 + R6 = 85
; матрица контурных сопротивлений
Z = |
Z11 -Z12 -Z13
-Z21 Z22 -Z23
-Z31 -Z32 Z33
|
; значения контурных ЭДС источников
Ek1 = E1 = 80
Ek2 = - E2 = -50
Ek3 = E3 = 60
; матрица ЭДС источников (контурных ЭДС)
E = |
Ek1
Ek2
Ek3
|
Zrev = revM(Z) ; вычисление реверсивной матрицы контурных сопротивлений
I = |Zrev*E| ; вычисление контурных токов (решение системы уравнений)
; вывод значений контурных токов
valM(I) : I = |2.72699, 1.26373, 2.18871|
; расчет значений токов ветвей
I1 = I[1,1] = 2.72699
I2 = - I[2,1] = -1.26373
I3 = I[3,1] = 2.18871
I4 = I[1,1] - I[2,1] = 1.46326
I5 = I[1,1] - I[3,1] = 0.53828
I6 = -I[2,1] + I[3,1] = 0.92498
;
;------------ ПРОВЕРКА РАСЧЁТА ---------------
;----------- ЭНЕРГОБАЛАНС -------------
Pe = E1*I1 + E2*I2 + E3*I3 = 286.29544
Pi = I1^2*R1 + I2^2*R2 + I3^2*R3 + I4^2*R4 + I5^2*R5 + I6^2*R6 = 286.29544
Если ввести данную программу в окно калькулятора, то получим значения, которые подставятся при вычислении непосредственно в тексте программы после второго знака равно. Если изменить исходные значения ЭДС и сопротивлений, изменятся и расчётные значения.
Для проверки правильности расчёта вычисляется баланс мощностей. Суммарная мощность, затрачиваемая от источников Pe, должна быть равна суммарной мощности, выделяемой на пассивных элементах цепи Pi. В данном случае, как видим, так оно и есть.
Листинг программы на Mathcad доступен здесь
Практическая задача на переменном токе
В качестве практического применения метода контурных токов на переменном токе рассмотрим следующую схему.| Рис.3 |
Данная схема представляет собой фильтр нижних частот (ФНЧ), рассмотренный в разделе . Для частоты среза 100 Гц ФНЧ имеет следующие величины:
R1 = 318 Ом – сопротивление источника
Rn = R1 = 318 Ом – сопротивление нагрузки
C1 = C2 = 5 мкФ (5Е-6 Ф)
L1 = 1.013 Гн
В том же разделе была вычислена амплитудно-частотная характеристика (АЧХ) данного фильтра по аналитической формуле. Здесь с этой же целью мы применим метод контурных токов.
Для начала рассчитаем схему на одной частоте f = 100 Гц.
Обозначим :
ω = 2πf – круговая частота
Для схемы рис. 3 сопротивления ветвей будут рассчитываться как:
Z1 = R1
Z2 = - i/(ωC1)
Z3 = iωL1
Z4 = Z2
Z5 = Rn
Как видим значения сопротивлений источника R1 и нагрузки Rn – действительные числа, а сопротивлений Z2, Z3, Z4 – мнимые, где i – мнимая единица.
Программа расчета данной цепи для калькулятора KAN приведена ниже:
; Калькулятор KAN.
; Метод контурных токов. Переменный ток.
mas: Z[3,3], Zrev[3,3], E[3,1], I[3,1] ; декларирование массивов для элементов матриц
;--------------------- ДАНО: --------------------------------
C1 = 5E-6
C2 = C1
L = 1.013
f = 100 ; частота
w = 2*pi*f ; круговая частота
; сопротивления ветвей
R1 = 318 ; сопротивление источника
Z1 = R1
Z2 = -!/(w*C1); комплексное сопротивление ёмкости C1
Z3 = !(w*L); комплексное сопротивление индуктивности L
Z4 = Z2
Z5 = R1 ; сопротивление нагрузки
; значения ЭДС источников (контурные ЭДС)
E1 = 1
;------------------------- РАСЧЁТ -------------------------------
format(dec,5) ; формат выводимых чисел
; значение контурных сопротивлений
Z11 = Z1 + Z2
Z12 = Z2
Z13 = 0
Z21 = Z2
Z22 = Z2 + Z3 + Z4
Z23 = Z4
Z31 = 0
Z32 = Z4
Z33 = Z4 + Z5
; матрица контурных сопротивлений
Z = |
Z11 -Z12 -Z13
-Z21 Z22 -Z23
-Z31 -Z32 Z33
|
; матрица ЭДС источников (контурных ЭДС)
E = |
E1
0
0
|
Zrev = revM(Z) ; вычисление реверсивной матрицы контурных сопротивлений
I = |Zrev*E| ; вычисление контурных токов (решение системы уравнений)
; вывод значений контурных токов
valM(I) : I = |0.00079+!0.00079, 3.28230E-7-!0.00157, -0.00079-!0.00079|
; расчет комплексных значений токов ветвей
I1 = I[1,1] = 0.00079+!0.00079
I2 = I[1,1] - I[2,1] = 0.00079+!0.00236
I3 = I[2,1] = 3.28230E-7-!0.00157
I4 = I[2,1] - I[3,1] = 0.00079-!0.00078
I5 = I[3,1] = -0.00079-!0.00079
; расчет амплитудных значений токов ветвей (их модулей)
I1m = modC(I1) = 0.00111
I2m = modC(I2) = 0.00248
I3m = modC(I3) = 0.00157
I4m = modC(I4) = 0.00111
I5m = modC(I5) = 0.00111
; расчет напряжения на сопротивлении нагрузки
Un = I[3,1]*Z5 = -0.24976-!0.2501
; расчет коэффициента передачи (передаточная функция цепи)
K = Un/E1 = -0.24976-!0.2501
K = modC(K) = 0.35346 ; модуль коэффициента передачи
K_db = 20*lg(K) = -9.03332 ; модуль коэффициента передачи в децибелах
;
;----------- ПРОВЕРКА РАСЧЕТА. ЭНЕРГОБАЛАНС -------------
Pe = E1*I1 = 0.00079+!0.00079
Pi = I1^2*Z1 + I2^2*Z2 + I3^2*Z3 + I4^2*Z4 + I5^2*Z5 = 0.00079+!0.00079
; Метод контурных токов. Переменный ток.
mas: Z[3,3], Zrev[3,3], E[3,1], I[3,1] ; декларирование массивов для элементов матриц
;--------------------- ДАНО: --------------------------------
C1 = 5E-6
C2 = C1
L = 1.013
f = 100 ; частота
w = 2*pi*f ; круговая частота
; сопротивления ветвей
R1 = 318 ; сопротивление источника
Z1 = R1
Z2 = -!/(w*C1); комплексное сопротивление ёмкости C1
Z3 = !(w*L); комплексное сопротивление индуктивности L
Z4 = Z2
Z5 = R1 ; сопротивление нагрузки
; значения ЭДС источников (контурные ЭДС)
E1 = 1
;------------------------- РАСЧЁТ -------------------------------
format(dec,5) ; формат выводимых чисел
; значение контурных сопротивлений
Z11 = Z1 + Z2
Z12 = Z2
Z13 = 0
Z21 = Z2
Z22 = Z2 + Z3 + Z4
Z23 = Z4
Z31 = 0
Z32 = Z4
Z33 = Z4 + Z5
; матрица контурных сопротивлений
Z = |
Z11 -Z12 -Z13
-Z21 Z22 -Z23
-Z31 -Z32 Z33
|
; матрица ЭДС источников (контурных ЭДС)
E = |
E1
0
0
|
Zrev = revM(Z) ; вычисление реверсивной матрицы контурных сопротивлений
I = |Zrev*E| ; вычисление контурных токов (решение системы уравнений)
; вывод значений контурных токов
valM(I) : I = |0.00079+!0.00079, 3.28230E-7-!0.00157, -0.00079-!0.00079|
; расчет комплексных значений токов ветвей
I1 = I[1,1] = 0.00079+!0.00079
I2 = I[1,1] - I[2,1] = 0.00079+!0.00236
I3 = I[2,1] = 3.28230E-7-!0.00157
I4 = I[2,1] - I[3,1] = 0.00079-!0.00078
I5 = I[3,1] = -0.00079-!0.00079
; расчет амплитудных значений токов ветвей (их модулей)
I1m = modC(I1) = 0.00111
I2m = modC(I2) = 0.00248
I3m = modC(I3) = 0.00157
I4m = modC(I4) = 0.00111
I5m = modC(I5) = 0.00111
; расчет напряжения на сопротивлении нагрузки
Un = I[3,1]*Z5 = -0.24976-!0.2501
; расчет коэффициента передачи (передаточная функция цепи)
K = Un/E1 = -0.24976-!0.2501
K = modC(K) = 0.35346 ; модуль коэффициента передачи
K_db = 20*lg(K) = -9.03332 ; модуль коэффициента передачи в децибелах
;
;----------- ПРОВЕРКА РАСЧЕТА. ЭНЕРГОБАЛАНС -------------
Pe = E1*I1 = 0.00079+!0.00079
Pi = I1^2*Z1 + I2^2*Z2 + I3^2*Z3 + I4^2*Z4 + I5^2*Z5 = 0.00079+!0.00079
Пояснения даны в виде комментариев. Комплексное число вида a + ib записывается на языке KAN как a + !b. Как видно из текста программы модуль коэффициента передачи на частоте 100 Гц составил около -9 дБ, что соответствует результату полученному в разделе расчета АЧХ для этой частоты.
Для проверки правильности расчёта вычисляется баланс мгновенных мощностей. Суммарная мощность, затрачиваемая от источников Pe, должна быть равна суммарной мощности, выделяемой на пассивных элементах цепи Pi. В данном случае, так оно и есть.
Особо поясним строку:
E1 = 1.
Эта запись не означает, что взято постоянное напряжение равное 1 вольту. В данном случае напряжение переменное и в комплексной форме записывается как:
E1 = Aeiφ,
где A – амплитуда, а φ = ωt + φ0 - мгновенная фаза гармонического сигнала. Причем A = 1, φ = 0. Запись E1 = 1, соответствует этому случаю. Если бы мы рассматривали случай с ненулевой фазой, например φ = π/4 и амплитудой 1 вольт, мы данную строку записали бы так:
E1 = exp(!pi/4)
что соответствовало бы математической записи гармонического сигнала в комплексном виде:
E1 = eiπ/4
Соответственно комплексные значения токов и других комплексных величин получились бы другими, тогда как их модули, а так же модуль передаточной функции K и его логарифмическое значение K_db остались бы неизменными.
Данную программу нетрудно применить для произвольной ЛЭЦ, заменив размерность матриц (в директиве mas: число 3 заменяется на другое число контуров) и подставив соответствующие значения сопротивлений ветвей Zm и контурных ЭДС Ek.
В приведённой выше программе, помимо расчета токов ветвей цепи рис. 3, было получено значение АЧХ фильтра в одной точке f=100 Гц, равное примерно -9 дБ.
Листинг программы на Mathcad доступен здесь
Теперь модифицируем программу, чтобы, используя метод контурных токов, рассчитать АЧХ ФНЧ, представленного на рис. 3, в диапазоне частот.<
; Калькулятор KAN.
; метод контурных токов. Расчет АЧХ ФНЧ
mas: Z[3,3], Zrev[3,3], E[3,1], I[3,1] ; декларирование массивов для элементов матриц
;--------------------- ДАНО: --------------------------------
R1 = 318 ; сопротивление источника
C1 = 5E-6
C2 = C1
L = 1.013
; значения ЭДС источников (контурные ЭДС)
E1 = 1
; матрица ЭДС источников (контурных ЭДС)
E = |
E1
0
0
|
; матрица контурных сопротивлений
Z = |
Z11 -Z12 -Z13
-Z21 Z22 -Z23
-Z31 -Z32 Z33
|
;------------------------- РАСЧЁТ -------------------------------
format(dec,5) ; формат выводимых чисел
[f = 0:1000,10 ; цикл по частоте fmin:fmax, df
{f=0 f = 0.0001} ; для исключения деления на 0 при вычислении Z2
w = 2*pi*f ; круговая частота
; сопротивления ветвей
Z1 = R1
Z2 = -!/(w*C1)
Z3 = !(w*L)
Z4 = Z2
Z5 = R1 ; сопротивление нагрузки
; значение контурных сопротивлений
Z11 = Z1 + Z2
Z12 = Z2
Z13 = 0
Z21 = Z2
Z22 = Z2 + Z3 + Z4
Z23 = Z4
Z31 = 0
Z32 = Z4
Z33 = Z4 + Z5
Zrev = revM(Z) ; вычисление реверсивной матрицы контурных сопротивлений
I = |Zrev*E| ; вычисление контурных токов (решение системы уравнений)
Un = I[3,1]*Z5 ; расчет напряжения на сопротивлении нагрузки
K = Un/E1 ; расчет коэффициента передачи (передаточная функция цепи)
K = modC(K) ; модуль коэффициента передачи
K_db = 20*lg(K) ; модуль коэффициента передачи в децибелах
val(f, K_db); вывод значений АЧХ в таблицу и на график
]; завершение цикла
grafY(-50,0) ; задание пределов по оси Y
grafX(0,500) ; задание пределов по оси X
; метод контурных токов. Расчет АЧХ ФНЧ
mas: Z[3,3], Zrev[3,3], E[3,1], I[3,1] ; декларирование массивов для элементов матриц
;--------------------- ДАНО: --------------------------------
R1 = 318 ; сопротивление источника
C1 = 5E-6
C2 = C1
L = 1.013
; значения ЭДС источников (контурные ЭДС)
E1 = 1
; матрица ЭДС источников (контурных ЭДС)
E = |
E1
0
0
|
; матрица контурных сопротивлений
Z = |
Z11 -Z12 -Z13
-Z21 Z22 -Z23
-Z31 -Z32 Z33
|
;------------------------- РАСЧЁТ -------------------------------
format(dec,5) ; формат выводимых чисел
[f = 0:1000,10 ; цикл по частоте fmin:fmax, df
{f=0 f = 0.0001} ; для исключения деления на 0 при вычислении Z2
w = 2*pi*f ; круговая частота
; сопротивления ветвей
Z1 = R1
Z2 = -!/(w*C1)
Z3 = !(w*L)
Z4 = Z2
Z5 = R1 ; сопротивление нагрузки
; значение контурных сопротивлений
Z11 = Z1 + Z2
Z12 = Z2
Z13 = 0
Z21 = Z2
Z22 = Z2 + Z3 + Z4
Z23 = Z4
Z31 = 0
Z32 = Z4
Z33 = Z4 + Z5
Zrev = revM(Z) ; вычисление реверсивной матрицы контурных сопротивлений
I = |Zrev*E| ; вычисление контурных токов (решение системы уравнений)
Un = I[3,1]*Z5 ; расчет напряжения на сопротивлении нагрузки
K = Un/E1 ; расчет коэффициента передачи (передаточная функция цепи)
K = modC(K) ; модуль коэффициента передачи
K_db = 20*lg(K) ; модуль коэффициента передачи в децибелах
val(f, K_db); вывод значений АЧХ в таблицу и на график
]; завершение цикла
grafY(-50,0) ; задание пределов по оси Y
grafX(0,500) ; задание пределов по оси X
Теперь расчёт осуществляется в цикле изменением частоты f. Если ввести данную программу в окно калькулятора, то получим таблицу значений АЧХ K_db в децибелах и график, который представлен ниже.
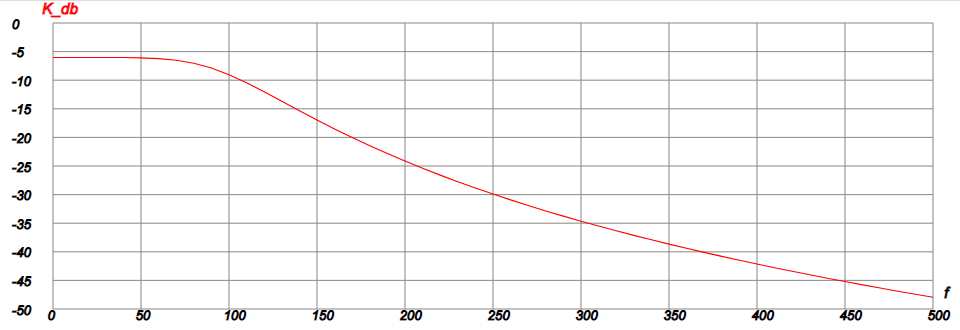 |
| Рис.4 |
Сравнивая этот график с графиком, полученным в другом разделе и совсем другим способом, приходим к выводу, что они совпадают.

|
Обратная связь: alexander.nekhaev53@gmail.com |

|
Поддержать проект |

|
Заказать расчет |