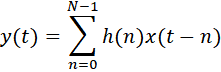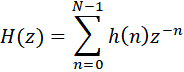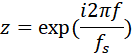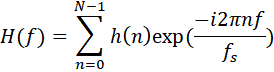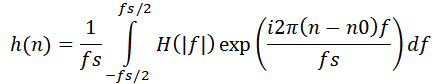На страницах нашего сайта:
Расчёт рекурсивных цифровых фильтров. Каскадная реализация. Расчёт рекурсивных цифровых фильтров. Прямая реализация.
были представлены методики расчётов рекурсивных (БИХ) цифровых фильтров.
Здесь мы рассматриваем класс нерекурсивных фильтров или по-другому фильтров с конечной импульсной характеристикой (КИХ). КИХ-фильтры имеют существенно больший порядок и соответственно большее количество вычислений по сравнению с БИХ-фильтрами, но обладают двумя значительными преимуществами:
1. КИХ-фильтры устойчивы к самовозбуждению, т.к. не содержат обратной связи. 2. КИХ-фильтры позволяют создать абсолютно линейную фазовую характеристику, что всегда желательно, а во многих случаях необходимо.
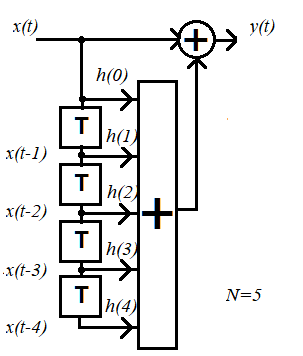
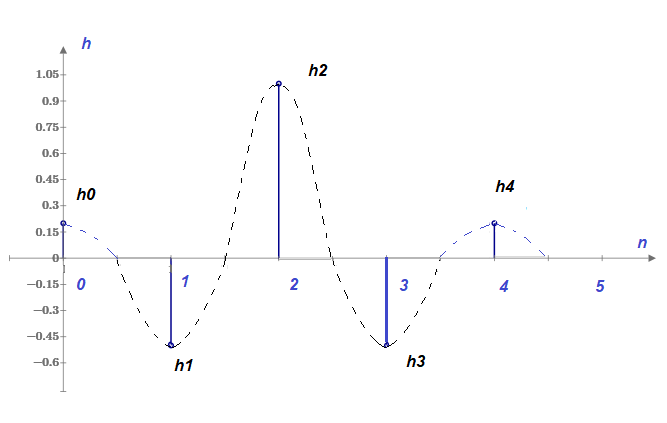
Не углубляясь в рассмотрение всех возможных вариантов КИХ-фильтров, приведём схему и импульсную характеристику h(n) фильтра, который обладает линейной фазовой характеристикой.
Рис. 1
T – элемент задержки на один период дискретизации.
Рис. 2
Заметим, что линейность фазовой характеристики обеспечивается при симметричной форме импульсной характеристики, такой, как на приведенном рисунке. В примере порядок фильтра N=5. При реализации на вычислительных устройствах работа такого фильтра задаётся следующим выражением:
y(t) = h(0)x(t)+h(1)x(t-1)+h(2)x(t-2)+h(3)x(t-3)+h(4)x(t-4),
где t – дискретное время в числах натурального ряда 0,1,2,3… и т.д., поскольку, рассматривая цифровые фильтры, мы имеем дело с цифровыми отсчётами непрерывного сигнала.
На практике же порядок КИХ-фильтра значительно больше. В общем виде во временной области работа фильтра описывается суммой (скользящее среднее или свёртка):
x(t-n) – значения входных отсчётов в линии задержки, состоящей из элементов T.
Передаточная характеристика КИХ-фильтра в частотной области выглядит следующим образом:
z-n – соответствует в частотной области задержке на n дискретных моментов времени. Учитывая, что
где fs=1/T – частота дискретизации, перейдём к виду:
Здесь exp(x)=ex.
Модуль данной передаточной характеристики представляет собой амплитудно-частотную характеристику (АЧХ) цифрового фильтра. Заметим, что формула (1) фактически представляет собой прямое дискретное преобразование Фурье импульсной характеристики h(n). Это означает, что саму импульсную характеристику, т.е. коэффициенты КИХ-фильтра h(0), h(1), … h(N-1) можно получить непосредственно из заданной H(f) методом обратного преобразования Фурье, т.е. по формуле:
где n0 = (N-1)/2 – центральное значение n, относительно которого симметрично расположены левая и правая части импульсной характеристики h(n). Взятие модуля |f| предполагает, что H(f) – чётная функция относительно точки f=0.
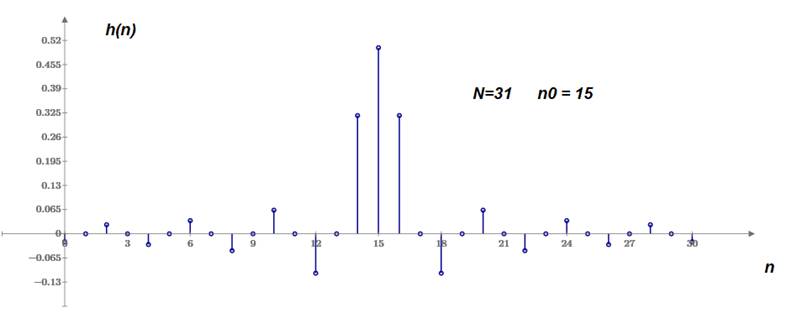
Типичный вид h(n) для N=31 показан ниже.
Рис. 3
Перейдём к практической задаче и на её примере рассмотрим основной подход к проектирования цифровых фильтров данного вида. Поставим задачу разработать КИХ-фильтр со следующими параметрами:
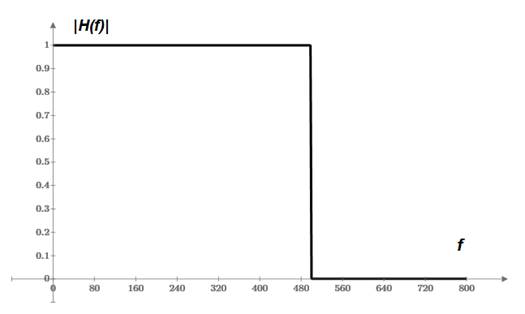
fc = 500 Гц - частота среза фильтра fr = 600 Гц - частота, с которой начинается заданное ослабление фильтра Kdb r Kdb c = - 6 dB - коэффициент передачи фильтра на частоте среза Kdb r = - 50 dB - коэффициент передачи (заданное ослабление) на частоте f>=fr
Начнём с самого простого: зададим модуль передаточной характеристики фильтра H(f) в виде прямоугольника:
Рис. 4
Подставив H(f) в формулу (2), получим импульсную характеристику h(n) как на рис. 3. Сразу заметим, что чем круче переход от полосы пропускания к полосе непропускания, тем больше потребуется коэффициентов h(n). В частности для прямоугольной H(f) импульсная характеристика h(n) убывает крайне медленно по закону sin(x)/x и резко обрывается в 0 левее h(0) и правее h(N-1), что приводит, как будет показано ниже, к большим пульсациям АЧХ. По этой причине на практике применяется метод «оконного взвешивания», который заключается в умножении h(n) на весовую функцию w(n), называемую «окном»:
hw(n) = h(n)w(n)
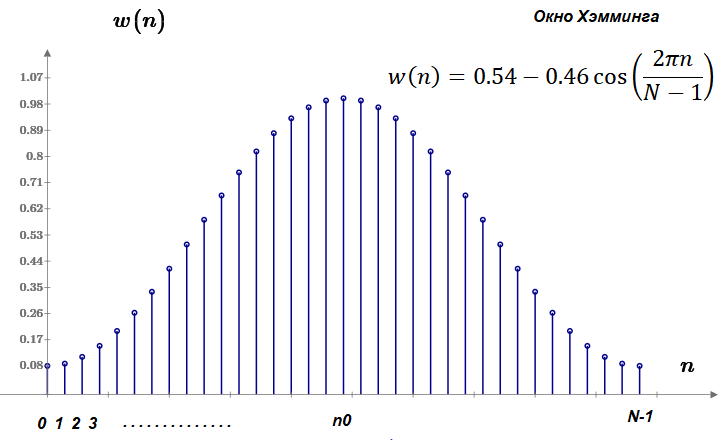
Часто применяется окно Хэмминга, для которого
Рис. 5
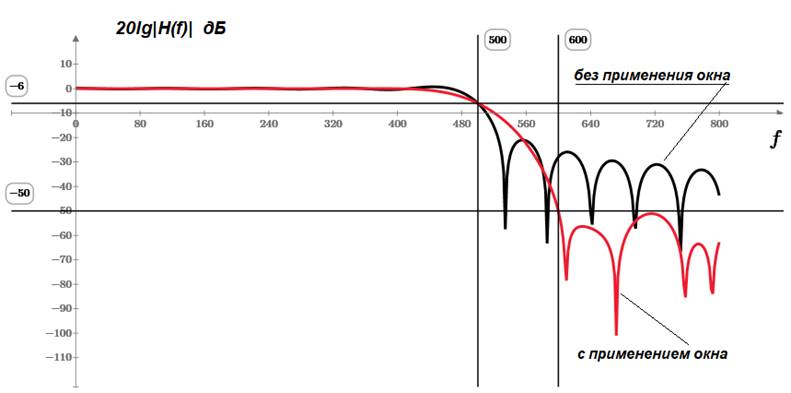
Применение окна, приводит к постепенному сведению «на нет» значений h(n) к крайним от центра n0 точкам. Этот приём даёт значительное улучшение АЧХ по сравнению с прямоугольным случаем, что видно на следующем рисунке:
Рис. 6
Заметим, что желаемый результат (-50 дБ в полосе непропускания) был получен с применение окна Хэмминга при N=35. Mathcad программа, с помощью которой получены данные результаты, имеется в платном доступе здесь Рассмотренный подход является далеко не единственным при проектировании нерекурсивных цифровых фильтров. С общей теорией можно познакомиться в книге Лэма [1], хотя существует множество других книг и учебных пособий, в частности, можно порекомендовать [2]. Практические аспекты хорошо освещены в [3] и [4]. Наконец, имеются бесплатные он-лайн сервисы по расчёту фильтров данного типа, например [5]. В литературе для обозначения КИХ-фильтра может также встретиться термин «трансверсальный». В заключение интересно было бы оценить, при каких порядках требования поставленной задачи достижимы для рекурсивных (БИХ) фильтров (см. ссылки в начале страницы). Как показывают расчёты, фильтр Чебышева аналогичную задачу может решить при N=12. Однако, учитывая, что БИХ-фильтр содержит как рекурсивную, так и нерекурсивную части, причём обе с числом коэффициентов равным N, то реальное число коэффициентов будет вдвое большим, т.е. 2N = 24 против 35. А если принять во внимание, что фазочастотная характеристика фильтра Чебышева далека от линейной, то можно сделать вывод, что при жестких требованиях к фильтрации предпочтительнее применение нерекурсивных, т.е. КИХ-фильтров.
Литература и ссылки1. Г. Лэм. Аналоговые и цифровые фильтры. Москва, Издательство Мир, 1982 2. Вадутов О.С. Лекции. Тема 9. Цифровые фильтры. 3. Расчет КИХ фильтра с линейной фазочастотной характеристикой 4. Функции оконного сглаживания 5. The free online IIR design tool
|