Расчет LC-фильтра нижних частот Баттерворта

На данной странице рассмотрены вопросы расчёта ФНЧ Баттерворта на калькуляторе КАН.
Mathcad-программа для расчета ФНЧ Баттерворта доступна по ссылке

Амплитудно-частотная характеристика

ФНЧ с аппроксимацией прямоугольной амплитудно-частотной характеристики (АЧХ) по Баттерворту характеризуется максимально плоской и монотонно спадающей АЧХ.
Аналитическая зависимость коэффициента передачи данного фильтра K(F) имеет вид:

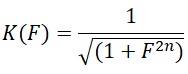
(1)

Где
F= f/fc - нормированная частота
f – частота,
fc – частота среза,
n – порядок фильтра

Графики K(F) для n = 1, 2 , 3 представлены на рис 1.

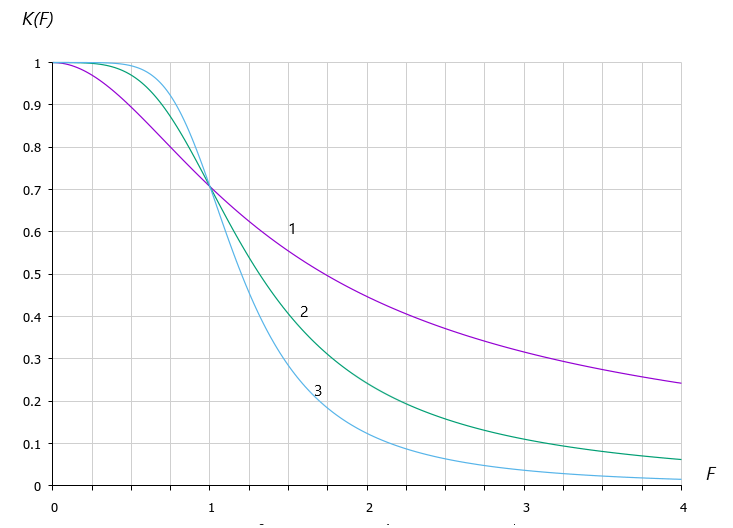
Рис. 1

Из графиков видно, что чем выше порядок фильтра n, тем более плоской становится АЧХ в полосе пропускания (F≤1) и более крутой за её пределами (F>1), приближаясь к прямоугольной.
На нулевой частоте коэффициент передачи равен 1. На частоте среза (F = 1) коэффициент передачи, как это следует из (1) равен:

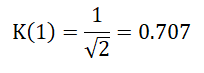
На практике АЧХ принято выражать в децибелах:
Kdb(F) = 20 lg K(F), где lg – десятичный логарифм.
Графики Kdb(F) для n = 1, 2 , 3 представлены на рис 2.

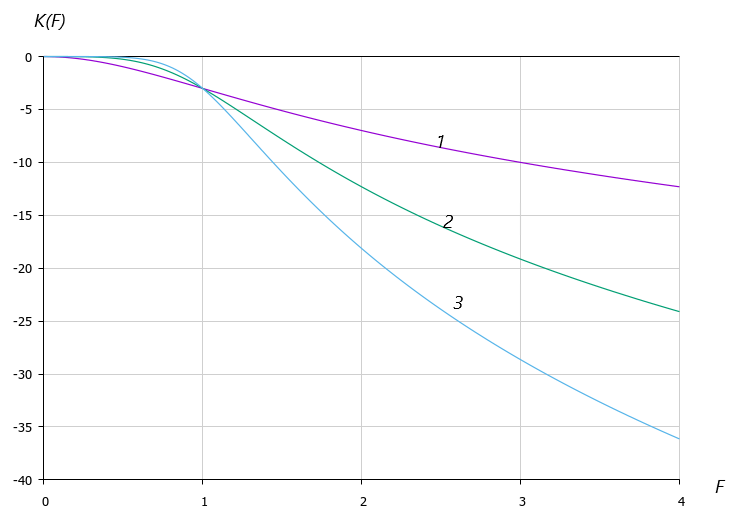
Рис. 2
На нулевой частоте коэффициент передачи равен 0 дБ. На частоте среза (F = 1) коэффициент передачи Kdb(1) равен – 3 дБ.
Спад АЧХ в области достаточно удалённой от частоты среза (F>2) составляет в зависимости от порядка фильтра:

n = 1, спад 6 дБ на октаву
n = 2, спад 12 дБ на октаву
n = 3, спад 18 дБ на октаву

В общем случае скорость спада для ФНЧ Баттерворта n*6 дБ/октава.
Фильтры, реализующие данный вид АЧХ, принято называть «фильтрами Баттерворта».
Заметим, что при n = 1 фильтр Баттерворта может быть реализован обычной RC – цепью:

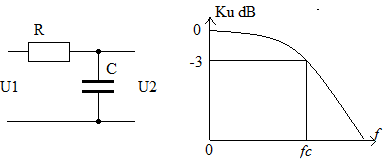
Рис. 3
Частота среза такого фильтра

Следующим по сложности, но уже с более крутым спадом, равным 12 дБ/октава, будет следующий фильтр.

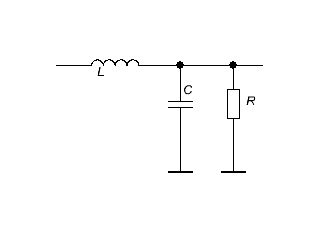
Рис. 4

Эта схему можно рассматривать как реализацию ФНЧ Баттерворта 2-го порядка при следующих значениях:

Задано:
fc – частота среза ФНЧ в Гц
С - емкость в Фарадах

Расчётные значения:

При этом предполагается, что выходное сопротивление предыдущего каскада или, как принято в теории, сопротивление источника, значительно меньше сопротивления R.
АЧХ K(f) можно рассчитать на калькуляторе KAN

Фрагмент программы показан ниже:

Кликните по нему, чтобы запустить программу.
В дальнейшем используйте данную программу, подставляя свои значения.
Как сохранять программу и её результаты описано здесь.

В программе задано:

fc = 100 - частота среза в Гц
C = 10 мкФ – емкость микрофарадах или 10E-6 в фарадах.
АЧХ в децибелах приведена ниже:

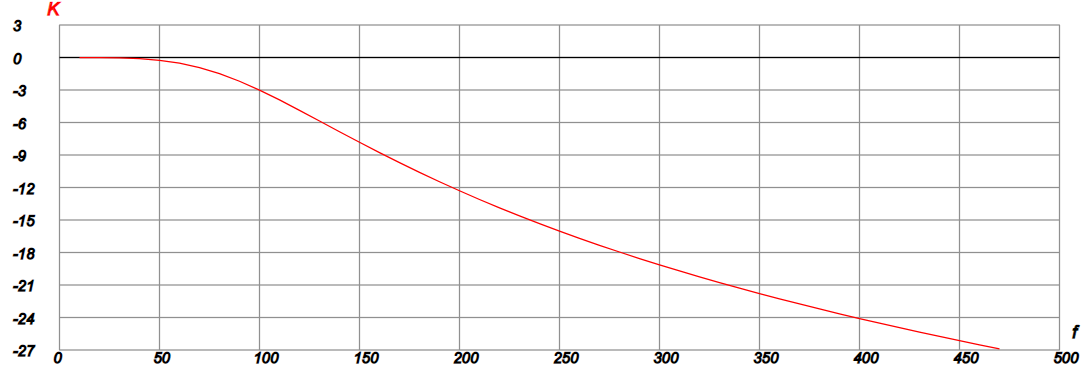
Рис. 5

Определение порядка многозвенного фильтра

Перейдем к общему случаю, когда требуется произвести расчёт при заданных значениях крутизны спада АЧХ. Для этого нужно определить порядок фильтра. Порядок фильтра n задает величину спада АЧХ в полосе подавления (непропускания). Соответственно он определяет и сложность фильтра. Для расчёта фильтра нижних частот принято задавать следующие параметры:
fc – частота среза фильтра и, соответственно, коэффициент передачи фильтра на этой частоте K_{db c}. Обычно принимается K_{db c} = - 3 dB, что соответствует K(1) = 0.707.
fr – частота, с которой начинается заданное ослабление фильтра K_{db r}
Исходя из этих параметров, вычисляется порядок фильтра Баттерворта:

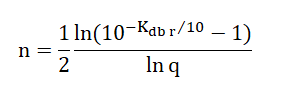(2)

Эта формула выводится из формулы (1).
Где q = fr / fc . Очевидно, что всегда q > 1.
Число n округляется вверх до ближайшего целого.
В качестве примера определим порядок фильтра, задав следующие значения:
fc = 100 Гц
fr = 200 Гц
K_{db c} = - 3 dB
K_{db r} = - 30 dB
Подставляя эти значения в формулу (2) и воспользовавшись калькулятором KAN, получим n = 5.

; KAN

; программа расчёта порядка фильтра Баттерворта

fc = 100 ; частота среза ФНЧ

fr = 200 ; частота требуемого начального ослабления в полосе подавления

Kr = -30 ; требуемое начальное ослабление в полосе подавления

q = fr/fc = 2 

n = 1/2*ln(10^(-Kr/10) - 1)/ln(q) = 4.98217 ; дробное значение порядка фильтра

n = int(n) + 1 = 5 ; значение порядка фильтра, округлённое до целого вверх

Можно скопировать данную программу в окно калькулятора и, подставляя другие значения, использовать её в своих расчетах.

Реализация LC-фильтра нижних частот Баттерворта

Перейдем к реализации ФНЧ Баттерворта. Причём реализаций может быть множество, например, на LC-элементах, на операционных усилителях, на переключаемых конденсаторах, на цифровых вычислительных устройствах и др. Здесь мы ограничимся реализацией на LC- элементах, т.е. на катушках индуктивности и конденсаторах. Опуская математическую сторону вопроса (см. [1]), приведем два вида реализации фильтра Баттерворта на LC-элементах.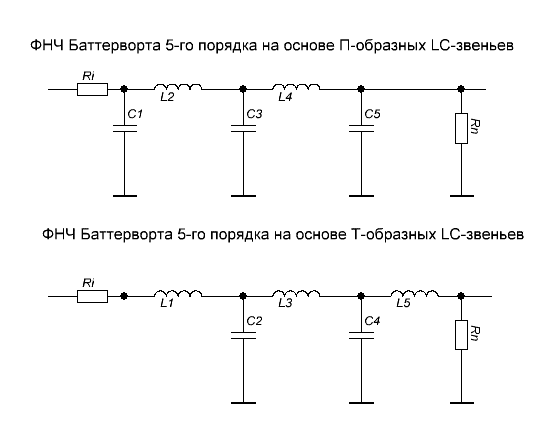

Рис. 6 ФНЧ Баттерворта 5-го порядка на основе П- и Т-образных LC-звеньев

На рис. 6 показаны два варианта реализации ФНЧ Баттерворта 5-го порядка на основе П- и Т- образных LC-звеньев.
Обратите внимание, что нумерация элементов общая для L и C. Так удобно для расчетов. Закономерность построения схем достаточно простая, чтобы построить фильтр любого порядка. Заметим также, что для ФНЧ Баттерворта порядок фильтра равен количеству LC-элементов. Сопротивления источника Ri и нагрузки Rn берутся не произвольным образом. Их значения связаны с величинами элементов L и C. При произвольных значениях Ri и Rn фильтр будет не согласован и его АЧХ будет отличаться от желаемой. Заметим также, что на нулевой частоте схемы вырождаются в простой резистивный делитель напряжения на резисторах Ri и Rn. Обычно принимают Ri = Rn. При равенстве Ri и Rn коэффициент передачи будет равен ½ или -6 дБ. Это означает, что на частоте среза он должен быть равным: -6 – 3 = -9 дБ.
В теоретической литературе принято рассчитывать фильтр предварительно для значений R = 1 Ом и

рад/сек (соответствует

Гц ). Такой фильтр называется нормированным. В [1] для первой схемы приведены следующие формулы нормированного ФНЧ Баттерворта:

, где m – нечетно,

, где m – четно.

Для второй схемы Cm и Lm меняются местами:

, где m – нечетно,

, где m – четно.
Значения получаются в Гн (Генри) для Lm и в Ф (Фарадах) для Cm.
Далее их следует привести к значениям реального фильтра, для которого должно быть задано:
fc - требуемая частота среза в Гц.
R – требуемое сопротивление нагрузки ( источника).
Формулы для перерасчетa следующие:

Стставим программу для расчёта ФНЧ Баттерворта для обоих вариантов схемы и n = 5, fc = 100 Гц, R = 1000.

Фрагмент программы показан ниже:

Кликните по нему, чтобы запустить программу.
В дальнейшем используйте данную программу, подставляя свои значения.
Как сохранять программу и её результаты описано здесь.

Получите результат в виде таблицы:

---------------- Таблица данных ------------
 стр.  m         C         L         LL        CC       
 1     1.000E+0  9.836E-7  0.000E+0  9.836E-1  0.000E+0 
 2     2.000E+0  0.000E+0  2.575E+0  0.000E+0  2.575E-6 
 3     3.000E+0  3.183E-6  0.000E+0  3.183E+0  0.000E+0 
 4     4.000E+0  0.000E+0  2.575E+0  0.000E+0  2.575E-6 
 5     5.000E+0  9.836E-7  0.000E+0  9.836E-1  0.000E+0

Значения C и L соответствуют первому варианту схемы, LL и CC – второму. m – номера элементов в схемах. Там, где значения равны нулю означает, что элементов с такими номерами m не существует. Изменяйте n, R и fc в данной программе для интересующих вас случаев.
Для проверки результатов расчёта желательно смоделировать полученный фильтр и убедиться в их правильности. Используем для этих целей бесплатный в настоящее время пакет моделирования MicroCap-12.
. Ниже приведены схемы расчитанных выше фильтров и графики их АЧХ.

Рис. 7 Схемы ФНЧ Баттерворта на П- и Т- звеньях LC в LTSpice IV.

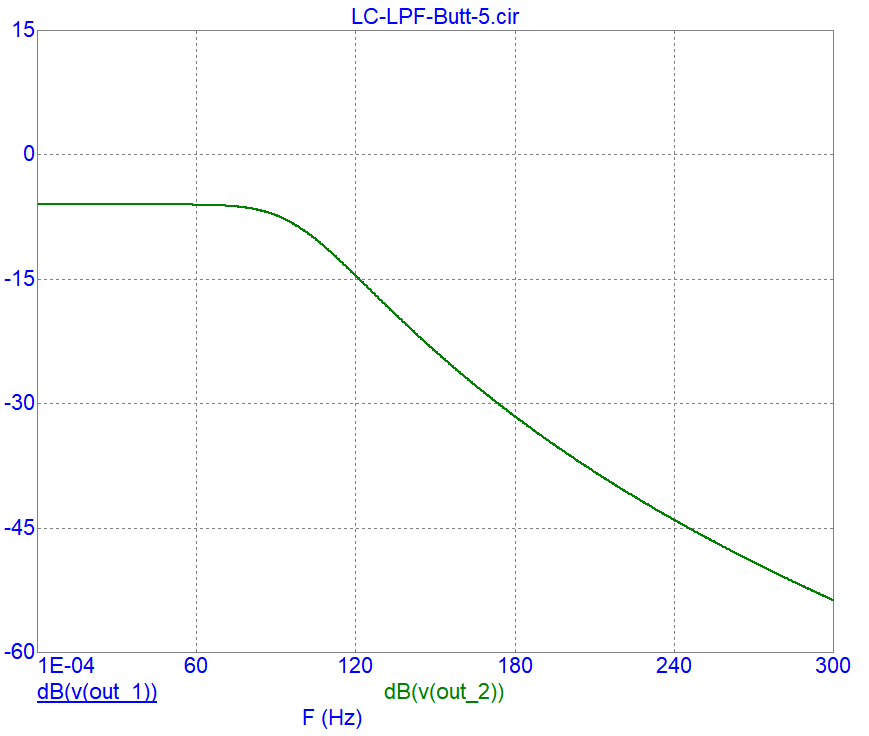
Рис. 8 АЧХ ФНЧ Баттерворта на П- и Т- звеньях LC

Обе характеристики совпадают. Как и требовалось в задании, срезы (-3 дБ относительно нулевой частоты или -9 дБ в абсолютном значении) находятся на частоте 100 Гц.

И в заключение приведём аналогичную программу, составленную в среде Mathcad для первого случая (сначала С).

Полный листинг Mathcad-программы доступен по ссылке

Литература.

Г. Лэм. Аналоговые и цифровые фильтры. Москва, Издательство Мир, 1982

Обратная связь:
alexander.nekhaev53@gmail.com

Поддержать проект

Заказать расчет