Уважаемые пользователи! Для корректности вычислений рекомендуем использовать браузеры следующих типов: Google Chrome, Opera и FireFox. К сожалению, популярные браузеры Internet Explorer и Microsoft Edge часто работают не корректно. Калькулятор разработан полностью на Google Chrome.Калькулятор КАН. Инструкция пользователя
Как пользоваться Операции Выражения Представление чисел Функции Встроенные константы Вычисление с переменными Вывод значений переменных. Оператор val() Формат выводимых чисел. Оператор format() Массивы Комплексные числа Циклы Оператор запрета вывода таблицы - noTab Графики Условный оператор Логические выражения Пользовательские функции Отладка программы. Оператор stop Матрицы и вектора Комментарии Сохранение программы и результатов расчёта Сводка операторов калькулятора КАН Данный калькулятор представляет собой сочетание редактора текста и калькулятора. В отличие от традиционных калькуляторов он позволяет вводить сложные числовые выражения, выражения с переменными, а также текстовые пояснения. С его помощью можно выполнять циклические программы. Поддерживаются действия над комплексными числами и матрицами. Калькулятор КАН можно также рассматривать как удобную среду программирования для решения типовых задач в математике, физике и в технических науках. Программу и результаты вычислений можно скопировать в редактор Word, сохранить и, при необходимости, скопировать обратно в окно калькулятора и продолжить вычисления. Калькулятор постоянно совершенствуется. Последняя версия выкладывается на сайте калькулятор.нехаев.рф.Как пользоваться
В простейшем случае введите числовое выражение и знак "=". Затем кнопку "Вычислить". Например, ввести выражение: 2+3= и нажать кнопку "Вычислить". В выражении допустимы пробелы. Признаком окончания выражения является знак "=", после которого на данной строке не должно быть никаких символов, кроме возможных комментариев, отделяемых от выражения точкой с запятой. 2+3 = ; по идее должно получиться 5, хотя, кто его знает?Операции
+ сложение - вычитание / деление * умножение ^ возведение в степеньВыражения
Пример простых выражений 2+3= 20/3= Виды выражений 1. Выражение вида 2 + 3 + ... = называется выражением арифметического типа. Оно должно заканчиваться знаком "=" , за которым может следовать комментарий. Действие калькулятора сводятся к вычислению данного выражения и выдачи результата после знака равно. В выражении допустимо использование переменных, значение которых должно быть присвоено ранее (т.е. выше по тексту программы). Например: x = 3 y = 7 2 + x + y = Другие примеры выражений арифметического типа: 3 + 3^2 - sin(30) = 1 + lg(10)/2 = cos(30 + x) = exp(-x/y) = Во всех случаях переменные в выражении должны быть определены ранее. В тригонометрических функциях не забываем устанавливать опции: "Угол градусах" либо "Угол в радианах". 2. Выражение вида x = 2 + 3 называется выражением присвоения. Действие калькулятора сводятся к вычислению выражения стоящего справа от знака равно и присвоению полученного значения переменной, стоящей слева от знака равно. Например, выражение x = x + 1 означает, что значение переменной в правой части увеличивается на 1 и новое значение присваивается этой же переменной. Примеры выражения присвоения: y1 = 3 + 3^2 - sin(30) x = 1 + lg(10)/2 fa1 = cos(30 + x) переменная_на_русском_языке = exp(-x/y) x = -x Во всех случаях переменные, стоящие в выражении справа от знака "=" , должны быть определены ранее, т.е. выше по тексту. Значение переменной присвоения, может быть использовано в последующих выражениях (в этом и смысл выражения присвоения). Значения переменных, может быть просмотрено с помощью оператора val(). Пример: x = 2 y = x + 3 val(x, y) Калькулятор выдаст: x = 2 y = x + 3 val(x, y): x = 2, y = 5 В цикловых конструкциях это не работает. В этом случае оператор val() применяется для вывода данных в таблицу, которая появится после выполнения программы. Вместо использования оператора val() можно в конце выражения поставить второй знак равно: x = 2 y = x + 3 = Калькулятор выдаст: x = 2 y = x + 3 = 5 2. Выражения вида 2 + 3 = 5 + 2 = 7 - 3 + 2= 6 ... и т.д. называются цепочными выражениями. Т.е. к результату можно добавлять новые члены, ставить знак "=" и затем нажимать кнопку "Вычислить". Цепочные выражения состоят из частных выражений. При изменении любого члена в любом частном выражении, пересчитывается вся цепочка выражений. Результаты расчётов частных выражений выделяются жирным шрифтом. Присваивать результат расчёта цепочного выражения переменной нельзя. Т.е. выражение присвоения типа x = 2 + 3 = 5 + 2 = 7 - 3 + 2= 6 работать не будет. Точнее калькулятор отбросит все частные выражения после второго знака "=" и присвоит переменной x значение равное 5.Представление чисел
Целые числа: Пример - 22345 Числа с дробной частью: Пример - 2.304 Экспоненциальное представление очень малых и очень больших чисел: Пример - 2.1E-5 (эквивалентно 0.000021), 2.1E+5 (эквивалентно 210000) Комплексное число типа 2 + i3 представляется в калькуляторе как 2 + !3 (см. ниже)Функции
^ - возведение в степень. Пример: 10^0.3 - (10 в степени 0.3) abs() - абсолютное значение числа. Пример: abs(-3) = 3 ln() - натуральный логарифм lg() - десятичный логарифм log(a,b) - логарифм a по основанию b exp() - экспонента. Работает как для действительных так и комплексных аргументов. int() - взятие целой части числа, int(2.67) = 2, int(-2.67) = -2 round() - округление числа до ближайшего целого, round(2.67) = 3, round(-2.67) = -3 sqr() - взятие квадратного корня mod(x,y) - = sqr(x^2 + y^2), где x, y - действительные числа modC(z) - модуль комплексного числа z = x + !y (соотв. z = x + iy) argC(z) - угол комплексного числа z = x + !y (соотв. z = x + iy) reC(z) - действительная часть комплексного числа imC(z) - мнимая часть комплексного числа parC(z1,z2) - значение параллельного сопротивления (в общем случае комплексного), parC(z1,z2) = z1*z2/(z1 + z2) sin() - тригонометрическая функция синус. cos() - тригонометрическая функция косинус tg() - тригонометрическая функция тангенс ctg() - тригонометрическая функция котангенс Угол в тригонометрических функциях можно представлять как в градусах, так и в радианах, для чего нужно установить соответствующую опцию на панели калькулятора (по умолчанию - в радианах). Для перевода углов из градусов в радианы и наоборот используются выражения: x(рад) = x(град)*pi/180 x(град) = x(рад)*180/pi В калькуляторе для удобства имеются встроенные функции: grad_to_rad() - переводит градусы в радианы rad_to_grad() - переводит радианы в градусы Совет. Представление угла в градусах используйте в простых, главным образом однострочных текстах; в многострочных текстах (программах) во избежание путаницы рекомендуется иметь дело с радианами. Обратные тригонометрические функции: arcsin() - функция, обратная синусу arccos() - функция, обратная косинусу arctg() - функция, обратная тангенсу arcсtg() - функция, обратная котангенсу Примечание. Обратные тригонометрические функции не однозначны: Равенства: arcsin(sin(x))=x, arctg(tg(x))=x - справедливы только для углов в интервале (-90,+90) Равенства: arccos(cos(x))=x, arcctg(ctg(x))=x - справедливы только для углов в интервале (0,180) Более подробно по тригонометрическим функциям см. здесь sh() - гиперболический синус ch() - гиперболический косинус th() - гиперболический тангенс cth() - гиперболический котангенс arsh() - обратный гиперболический синус arch() - обратный гиперболический косинус arth() - обратный гиперболический тангенс arcth() - обратный гиперболический котангенс Более подробно по гиперболическим функциям см. здесь fct() - факториал. fct(n) = n! = 1*2*...*n, где n - целое неотрицательное число (0! = 1, 1! = 1, 2! = 2, 3! = 6, ...) cmb(m,n) - число сочетаний (combinations). cmb(m,n) = n!/(m!*(n-m)!), причём m<=n prm(m,n) - число размещений (permutations). prm(m,n) = n!/(n-m)!, причём m<=n - здесь "!" - означает факториал. Примеры выражений, содержащих функции sqr(3^2 + 4^2)= (235 + ln(2))^0.25= sin(30) + cos(60)= В тригонометрических функциях не забываем устанавливать опции: "Угол градусах" либо "Угол в радианах".Встроенные константы
В калькуляторе имеется одна встроенная константа: pi = 3.141592653589793. Пример: sin(pi/2)=1 в данном случае угол представлен в радианах, pi/2 соответствует 90 градусам.Вычисление с переменными
Часто удобнее использовать выражения с символьными переменными, которые задаются перед выражением, т.е. выше него по тексту. Например: x = 2 y = 3 (x - y)/(x + y)= Здесь в числовом выражении пришлось бы дважды подставлять числовые значения переменных, причем делать это всякий раз при использовании других значений. Имя переменной может содержать несколько букв (латинских или кирилличных) и цифр, а также символ «_» (подчёркивание). Первым символом должна быть буква. Регистр (строчная, либо прописная буквы) имеет значение: X1 и x1 - это разные переменные. Последовательность строк с заданными переменными называется блоком. В приведенном примере блок состоит из трёх строк. Если после блока имеются две пустые строки, то все, что ниже них будет отсечено. Иными словами, в тексте программы допустимы только одиночные пустые строки.Вывод значений переменных. Оператор val()
Для вывода значений переменных, применяется оператор val(список_переменных). Пример: x = 2 y = x + 3 z = x + y val(x, y, z): x = 2, y = 5, z = 7 val вывел через запятую значения переменных, указанных в списке. Если оператор val() находится внутри цикла, то значения переменных выводятся в виде таблицы: [x=1:5 y = 2*x z = x^2 u = x^3 val(x,z,u) ] ---------------- Таблица данных ------------ стр. x z u 1 1 1 1 2 2 4 8 3 3 9 27 4 4 16 64 5 5 25 125 Максимальное количество столбцов в таблице равно 11. Поскольку первый столбец - это номера строк, то столбцов для значений переменных максимально 10. В цикле может быть только один оператор val(), поскольку результатом цикла является таблица, создаваемая этим оператором. Это ограничение действует и в том случае если цикл содержит вложенные циклы. Значения переменных, указанных в списке оператора val(), одновременно выводятся и на график ввиде зависимостей от переменной, указанной в списке первой. Если, по каким либо причинам, нет необходимости вывода значений той или иной переменной на график, то перед именем переменной следует установить звёздочку *. Например, если в указанном выше примере применить val(x,*z,u), то значения переменной z на график выводиться не будут.Формат выводимых чисел. Оператор format()
Формат выводимых чисел - десятичный или экспоненциальный, а также число знаков после запятой задаются опциями, расположенными под текстовым окном калькулятора. Иногда это не удобно, если часто пользоваться какой-либо программой, для которой ранее уже найден оптимальный способ отображения чисел. Для этого служит оператор format() Например, чтобы задать десятичный формат чисел с тремя знаками после запятой, оператор нужно задать в виде: format(dec,3) Число 33.33333333333333 отобразится в виде 33.333 Аналогично, чтобы задать экспоненциальный формат чисел с тремя знаками после запятой, оператор нужно задать в виде: format(exp,3) Число 33.33333333333333 отобразится в виде 3.333E+1 Оператор ставится в том месте программы, где нужно изменить формат выводимых чисел.Массивы
Массив - это переменная с индексом. Например: A[10], x1[k], B[n,m] Имена массивов объявляются в начале программы. mas: список_имен_массивов Пример: mas: A[100], B[200] ; в квадратных скобках указывается максимальный индекс k = 2 A[k]=2 B[4] = 3 x =A[k] + B[4] + 1 = Индекс массива, заключенный в квадратные скобки, может быть либо целым числом, либо переменной целого типа, либо выражением с результатом целого типа В КАН поддерживаются также двумерные массивы типа A[n,m]. Число массивов ограничено 10-ю. Индексы массивов могут принимать значения от 0 до максимального индекса. Индексом массива может быть либо целое число, либо выражение, например A[i+k+j], значением которого является целое число.Комплексные числа
Комплексное число типа 2 + i3 записывается в тексте калькулятора как 2+!3. Где символом ! (восклицательный знак) обозначена мнимая единица. Это сделано для того, чтобы избежать коллизий в случае, если имя переменной также начинается с буквы i. Возможна также запись комплексного числа в виде a#b, как это было принято в ранних версиях калькулятора КАН, но лучше в новых программах этого избегать. Например: Следующее выражение (2 + i3)*(3 + i2) + (3 + i5)/(1 + i2) = в калькуляторе следует представить как: (2 + !3)*(3 +!2) + (3 + !5)/(1 + !2) = результат: 2.6+!12.8 Чисто мнимое число, например i2.51, следует записать как !2.51 Просто мнимую единицу, как ! 1 + i, как 1 + ! Допустимы смешанные выражения типа: 2 + 2 + !3 + 2 = где 2 + !3 - комплексное число. Т.е. комплексные числа могут полноправно участвовать в операциях с действительными числами, однако хорошим правилом будет заключать их в скобки 2 + (2 + !3) + 2 = С комплексными числами допустимы стандартные арифметические операции +, -, *, /, а также возведение в действительную степень, в том числе и дробную. Например, выражение типа: (2 + !3)^(1/2) означает вычисление квадратного корня из комплексного числа 2 + !3. Эквивалентная запись sqr(2 + !3). Комплексное число может быть результатом извлечения квадратного корня из отрицательного действительного числа. Например: sqr(-4)= !2 На самом деле в данном случае существуют два корня:!2 и -!2. Калькулятор берет один из них и выдает сообщение в окне сообщений: "!!! В строке : sqr(-4)= при возведении в дробную степень возможен неоднозначный результат Примечание. Квадратный корень эквивалентен возведению в степень 1/2" Аналогичная ситуация при возведении отрицательного или комплексного числа в дробную степень. (-4 + !2)^0.5 = 0.486+!2.058 "!!! В строке : (-4 + !2)^0.5 = при возведении в дробную степень возможен неоднозначный результат" Дело в том, что для дробных степеней может существовать бесконечное число корней. КАН выбирает только один из них, а именно с индексом ноль в обобщённой формуле Муавра.Циклы
Цикл - это повторение блока выражений с разными значениями переменных. Применяется, например, при расчете арифметических функций. Пример, расчета функции извлечения корня: [x=0:5 y = sqr(x) val(x,y) ] Калькулятор выдаст и сам текст программы и таблицу: x y 0 0 1 1 2 1.41421 3 1.73205 4 2 5 2.23607 График функции будет показан в графическом окне калькулятора При желании таблицу можно скопировать в Excel (как см. ниже). Квадратные скобки означают начало и конец цикла. В приведенном выше примере используется цикл типа ОТ и ДО, аналог цикла for в языках программирования Общая конструкция такого цикла: [прм=прм1:прм2,шаг ............. ] Где прм – переменная цикла, прм1 и прм2 – числа соответствующие пределам вычисления (в общем случае это могут быть переменные и выражения). Допустимы отрицательные значения. Например x1 = 0 x2 = -5 [x= x1 : x2 y = x^2 val(x,y) ] x y 0 0 -1 1 -2 4 -3 9 -4 16 -5 25 Переменная цикла (в данном случае x) может изменяться только на +-1 Шаг - величина приращения цикла (по умолчанию либо 1, либо -1) Возможен другой тип цикла: цикл с выходом по условию. Оператор exit, выполняет выход из цикла. Общая конструкция такого цикла: [ ... {условие exit} ... ] Для приведенного выше случая эквивалентная программа с exit x1 = 0 x2 = -5 x = x1 [ y = x^2 val(x,y) {x=x2 exit} x = x - 1 ] x y 0 0 -1 1 -2 4 -3 9 -4 16 -5 25 Условие выхода из цикла может быть расположено в любом месте цикла. Таким образом, можно реализовывать все типы циклов, принятых в различных языках программирования: for, while, loop, until, do. Для вложенных циклов возможно использование оператора exitAll , который осуществляет выход из всех циклов и передает управление на строку, расположенную за самой нижней закрывающей квадратной скобкой: [ ... [ ... {условие exitAll} ... ] ... ] ;пример вложенного цикла [x=2:8,2 [y=1:4 z = x^2 + y val(x,y,z) ] ]Оператор запрета вывода таблицы - noTab
Иногда вывод таблицы не нужен. Например, когда представляет интерес только график. Запретить вывод таблицы можно оператором: noTab который должен располагаться в заключительной части программы (после оператора val). Пример: [x=1:5 y = 2*x z = x^2 val(x,y,z) ] noTabГрафики
В циклической программе значения переменных могут выводиться на график, причём в том же порядке, как они выводятся в таблицу: Пример: [x=1:5 y = 2*x z = x^2 val(x,y,z) ] ---------------- Таблица данных ------------ стр. x y z 1 1 2 1 2 2 4 4 3 3 6 9 4 4 8 16 5 5 10 25 На графике эта таблица отразится следующим образом: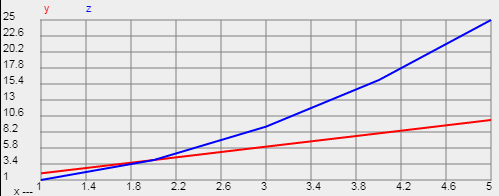
Первый столбец, обозначающий номера строк, на график не выводится. Второй столбец выводится по горизонтальной оси (ось X). Остальные столбцы выводятся в виде графиков по вертикальной оси (ось Y). Вверху графика выводятся имена переменных с цветами, соответствующим цветам графиков. Звездочка перед именем переменной в операторе val() запретит вывод значений этой переменной на график. Например, если в приведенноё выше программе записать val(x,*y,z), то значения переменной y на график выводиться не будут. Максимальное число выводимых переменных на график ограничено 6-ю. При этом, поскольку второй столбец соответсвует переменной выводимой на ось Х, то максимальное число графиков равно 5. Например, для оператора val(x1, x2, x3, x4, x5, x6, x7, x8, x9, x10) в таблицу будут выведены все переменные от x1 до x10, тогда как на график будут выведены x1, x2, x3, x4, x5, x6, где x1 - отразится по оси Х. Оператором val(x1, *x2, *x3, *x4, *x5, x6, x7, x8, x9, x10) на график будут выведены x1, x6, x7, x8, x9, x10. Пределы по осям X и Y определяются автоматически по максимальным и минимальным значениям вычисляемых данных. Диапазоны разбиваются на 10 и выводяться в виде цифр для линий сетки по шкале X и по шкале Y. При желании (например, чтобы увидеть на графике "красивые" цифры по осям X и Y) пределы можно задать принудительно с помощью операторов. grafX(x_min, x_max) , шаг сетки определяется как (x_max - x_min)/10 grafY(y_min, y_max), шаг сетки определяется как (y_max - y_min)/10 Если параметры в скобках заданы в виде чисел, то эти операторы могут располагаться в любом месте программы. Если параметры в скобках заданы в виде переменных (значение которых может изменятся по ходу программы), то эти операторы должны располагаться в конце программы. Существут также оператор: noGraf Данный оператор запрещает вывод графика и должен располагатся в заключительной части программы (после оператора val) Пример: [x=1:5 y = 2*x z = x^2 val(x,y,z) ] noGrafУсловный оператор
Условные оператор помещается в фигурных скобках и в общем случае имеет вид {условие выражение1 выражение2 ...... } Если условие выполняется, выполняются все последующие выражения в фигурных скобках. Если условие не выполняется, выполняются выражения или операторы, находящиеся после закрывающей фигурной скобки. Причем перед закрывающей скобкой на этой же строке не должно быть ничего, кроме пробелов. Пример: x = 0 [ y = 1 {x<4 y = 3} {x>=10 y = 5 } val(x,y) x = x + 1 {x>12 exit} ] В примере три условных оператора. Из них первые два модифицируют переменную y. Третий - выход из цикла. В процессе прохода цикла, переменная y примет следующие значения: y = 3, если x меньше 4 y = 5, если x больше либо равно 10 y = 1, если x больше либо равен 4, но меньше 10 Результатом будет таблица: x y 0 3 1 3 2 3 3 3 4 1 5 1 6 1 7 1 8 1 9 1 10 5 11 5 12 5 В данном примере применяется компактная форма условного оператора, когда весь условный оператор расположен на одной строке. В условном операторе применяются следующие операции сравнения: = равно > больше < меньше >= больше либо равно <= меньше либо равно <> или >< не равно Калькулятор поддерживает вложенные условные операторы - многострочные, типа: {условие1 .... {условие 2 ......... {условие3 ............ } ............ } .......... } и однострочные, типа: {условие1 {условие2 {условие3 оператор}}} Число вложений условных операторов неограниченно. В КАН нет конструкции ЕСЛИ условие ТО блок1 ИНАЧЕ блок2; Но её можно реализовать следующим образом: b = 0 {условие b = 1} {b = 1 блок1 } {b = 0 блок2 }Логические выражения
Условные операторы можно применять для замены логических выражений, которые в калькуляторе напрямую не поддерживаются. Например, выражение вида b = ((x>2) AND (x<4)) OR (x=0) где b - переменная, принимающая значения либо 0 (ложь), либо 1 (истина). запишем так: x = (какое-то значение) b = 0 {x>2 {x<4 b = 1}} {x=0 b = 1} val(b) Результат b = 1 будет при x = 3, либо при x = 0 и b = 0 в остальных случаях. Т.е. вложенные условные операторы соответствуют операции AND (И), а идущие по порядку друг за другом - операции OR (ИЛИ)Пользовательские функции
В случае если некоторое выражение используется в программе несколько раз, целесообразно объявить его в начале программы используя однострочную конструкцию: fun: имя_функции = выражение пример использования объявленных функций у и у1: fun: y = x^2 fun: y1 = y + 1 ; y - объявлена выше, такое допустимо x = 3 z = y + y1= u = 2*y + 3*y1 =Отладка программы. Оператор stop
Предназначен для отладки программы. Если в ходе выполнения программы возникают какие-то ошибки, то последовательное перемещение этого оператора позволяет определить на какой строке это происходит. На этом операторе вычисления заканчиваются и можно увидеть значения выражений и переменных. Например, в строке, где z3, произошло деление на 0. Последовательно перемещая вниз оператор stop, можно локализовать проблемную строку. x = 2 y = 3 u = 0 z1 = x + y = 5 z2 = 2*x + y = 7 stop; -------------------- Точка останова ---------------------- z3 = 2*(x+y)/u = z4 = (x+y)/2 = Его также можно использовать в цикле для просмотра текущих значений переменных. Для этого на строке с присвоением значения данной переменной нужно поставить второй знак "=". Сам оператор stop следует поместить внутри условного оператора, где условие задаёт момент останова в цикле: [x=1:10 x = x + 1 = 4 y = 2*x = 8 {x=4 stop}; -------------------- Точка останова ---------------------- val(x) ] После отладки всё лишнее можно удалить или задать заведомо невыполнимые условия: {2=1 stop} .Матрицы и вектора
Виды матриц, которые поддерживает калькулятор КАН Квадратная NxN Пример, при N = 3: 2 3 4 3 4 -1 2 5 0 В текстовом окне калькулятора записывается в строку следующим образом: A = |2 3 4, 3 4 -1, 2 5 0| где элементы в строках (столбцы) записываюися через пробел, строки же разделены запятыми Либо более привычным образом в многострочном виде: A = | 2 3 4 3 4 -1 2 5 0 | Число пребелов, один или более, роли не играет Прямоугольная NxM Пример, при N = 2, M = 3: 2 3 4 3 4 -1 Записывается в строку следующим образом: A = |2 3 4, 3 4 -1| или в многострочном виде: A = | 2 3 4 3 4 -1 | Эти операции называются инициализацией матрицы. Этим же способом можно инициализировать и массивы. Векторы Векторы - частные случаи матрицы. Вектор-строка: В = |2 3 4 -1 0| - есть матрица размерностью 1x5, состоящая из одной строки и 5-ти столбцов Вектор-столбец: В = |2,3, 4, -1, 0| - есть матрица размерностью 5x1, состоящая из 5-то строк одного столбца. Можно записать и так: В = | 2 3 4 -1 0 | Объявление (декларирование) матриц Во внутреннем представлении в КАН матрица эквивалентна двумерному массиву. Векторы так же представляют из себя массивы. Поэтому объявляется они аналогично объявлению массивов. mas: A[2,3]; - матрица размерностью 2х3 mas: B[1,4]; - вектор-строка ( = матрица размерностью 1x4 ) mas: С[4,1]; - вектор-столбец ( = матрица размерностью 4x1 ) Отдельные элементы матрицы также доступны, как и элементы массивов. Пример: mas: A[2,2] A[1,1] = 2 A[2,1] = 3 x = A[1,1] + A[2,1] = 5 Первая (верхняя) строка матрицы имеет индекс = 1, аналогично, первый (левый) столбец имеет индекс = 1 Элементы с индексами массивов, равными 0, в операциях с матрицами просто не используюся. Применительно к матрице: A = | 1 2 3 4 5 6 7 8 9 | если рассматривать её как двумерный массив имеем: A[1,1] = 1 A[1,2] = 2 A[1,3] = 3 A[2,1] = 4 ........... A[3,3] = 9 Операции над матрицами Поскольку элементы матрицы также доступны, как элементы массивов (т.к. матрица - это и есть двумерный массив), различные арифметические операции над матрицами можно делать аналогично обработке массивов, имея дело с отдельными элементами A[i, j]. Однако это неудобно. Поэтому КАН поддерживает специальные операции над матрицами Над матрицами возможны операции сложения, вычитания, умножения и умножения на число. Причем числа могут быть как действительными, так и комплексными. -присвоение B = |A| -Сложение и вычитание С = |A+B| С = |A-B| В этом случае матрицы должны быть одной размерности NxM -Умножение на число (или переменную целого типа) B = |3*A| - Умножения матрицы на матрицу C = |A*B| Операции умножения матриц не перестановочны! Т.е. |A*B| не равно |B*A|. При этом матрицы должны быть согласованы: ширина первой матрицы должна быть равна высоте второй матрицы. Т.е. размерности должны быть такими:Квадратные матрицы NxN этому условию удовлетворяют «автоматически», т.к для них: N1=M1=N2=M2=N3=M3. Все перечисленные матричные операции допускают только одну операцию в выражении. Например, выражения типа D = |A + B + C| - в КАН не поддерживаются. Обходимся так: D = |A+B| D = |D+C| Широко распространён частный случай этих операций: умножение матрицы или вектор-строки на вектор столбец. Кроме того для операций с матрицами применяются специальные функции: x = detM(A); - вычисление определителя матрицы, где х - число, в общем случае комплексное B = revM(A); - обращение (реверсирование) матрицы, где В матрица той же размерности, что и А valM(A) - вывод матрицы в виде строки: A = |2 3 4, 3 4 -1| valM(A) : A = |2 3 4, 3 4 -1| Одельные элемены матрицы можно выводить с помощью оператора val() как элементы массива: val(A[1,2], B[2,3]) Применение матриц Одно из применений матричной алгебры является решение систем линейных алгебраических уравнений (СЛАУ). Например, для СЛАУ второго порядка задано уравнение : x1 + 2*x2 = 8 2*x1 + 3*x2 = 18 Программа будет иметь вид: ; решение системы линейных уравнений (СЛАУ) mas: A[2,2], X[2,1], C[2,1], Arev[2,2] ;декларируем матрицы A=|1 2, 3 4| ; матрица коэффициентов a11, a12, .... C = |8,18|; коэффициенты в правой части - с1, с2, ... ;Теперь решаем СЛАУ Arev = revM(A); обращаем матрицу коэффициентов A --> Arev X = |Arev*C|; перемножаем Arev*С valM(X) : X = |2,3|; получаем решение - х1, x2, ,,, Решение: x1 = 2 x2 = 3 Эту программу можно переделать и для комплексных чисел.
Комментарии
Текстовые пояснения (комментарии) можно вводить после знака ";". Примеры: ;Расчеты по теореме Пифагора a=4 ; один катет прямоугольного треугольника b=5 ; второй катет прямоугольного треугольника ; гипотенуза sqr(a^2 + b^2)= ;результатСохранение программы и результатов расчёта
Как сохранять программу расчётов К сожалению, браузерные программы, каковой является калькулятор КАН, не позволяют сохранять пользовательские файлы напрямую. Тем не менее, есть несколько способов. Первый способ - это сохранить в Блокноте (встроенный сервис калькулятора). Для этого достаточно выделить программу в текстовом окне калькулятора, нажать клавиши Ctrl+C, открыть по ссылке Блокнот и с помощью клавиш Ctrl+V скопировать в него свою программу. После чего страницу Блокнота можно закрыть. Программа сохранится. Эта и другие программы, сохраненные ранее в Блокноте, будут постоянно храниться на вашем компьютере. Заметим, что «хранилище» у каждого браузера своё и где оно расположено только ему известно. Следующий более надежный способ сохранения – это в любом текстовом редакторе с последующей записью в файл. Например в стандартном текстовом редакторе ОС Windows,который также называется Блокнот. Разметка программы будет при этом утеряна, но она восстановится при обратном копировании и запуске на Вычисление. Можно так же нажать кнопку Разметка. Для копирования используем клавиши Ctrl+C и Ctrl+V. Наконец, программы можно сохранять в редакторе Word. Разметка сохраниться, но Word может изменить табуляцию, если она есть в вашей программе. В этом случае для правильного копирования из Word обратно в калькулятор, нужно скопировать из Word в буфер (Ctrl+C) войти в текстовое окно калькулятора и нажав правую кнопку мыши выбрать пункт контекстного меню «Вставить как обычный текст», либо использовать сочетание клавиш Ctrl+Shift+V. Как сохранять результаты расчётов Результатом расчётов обычно является таблица. Заметим, что по умолчанию (стоит галочка в квадратике «выравнивать таблицу») таблица выравнивается пробелами. В том случае, если необходимо скопировать таблицу, например, в Excel, чтобы использовать эти данные для дальнейшей обработки, в частности, для построения своих собственных графиков, перед вычислениями эту галочку необходимо снять. В этом случае столбцы разделяются не пробелами, а стандартными табуляторами. При этом таблица может выглядеть не так ровно, как в первом случае, но её можно корректно скопировать в Excel. При этом нужно учесть, что копировать следует не просто Ctrl+V, а установив в Excel курсор на нужную клетку, нажать правую клавишу, затем в открывшимся контекстном меню выбрать «Параметры вставки. Специальная вставка» и далее «Текст в кодировке Unicode». В этом случае в Excel таблица отобразиться правильно. Как сохранять графики Не все браузеры позволяют сохранить график (а это просто картинка) в графическом файле. В последних версиях ОС Windows есть стандартная программа Ножницы, которая позволяет легко это сделать.Сводка операторов калькулятора КАН
val(список_переменных) - в обычном режиме - вывод значений переменных в одну строку; в циклическом режиме - вывод значений переменных в таблицу и на график valМ(имя_матрицы) - вывод значений элементов матрицы noTab - запрет вывода данных в таблицу noGraf - запрет вывода данных на график grafX(x_min, x_max) - установка минимального и максимального пределов по оси X grafY(y_min, y_max) - установка минимального и максимального пределов по оси Y format(dec, n) - установка десятичного формата выводимых данных, где n - число знаков после десятичной точки format(exp, n) - установка экспоненциального формата выводимых данных, где n - число знаков после десятичной точки {условие оператор_присвоения} - условный оператор stop - оператор останова программы (отладочный оператор) exit - оператор выхода из текущего цикла (используется вместе с условным оператором) exitAll - оператор выхода из всех циклов (используется вместе с условным оператором)