На главную     ↑ Выше

Метод узловых напряжений

Заказать расчет                

Элементы теории


Задача анализа линейной электрической цепи (ЛЭЦ) заключается в нахождении токов всех её ветвей, напряжений в узлах и на элементах цепи, в вычислении передаточной функции цепи и других её характеристик. Один из основных методов анализа ЛЭЦ – т.н. метод узловых напряжений. На следующем рисунке показана электрическая цепь, состоящая из двух источников ЭДС: E1, E2 (в общем случае переменного тока), пяти сопротивлений Z1, … , Z5 (в общем случае комплексных) и трёх узлов 0, 1, 2.
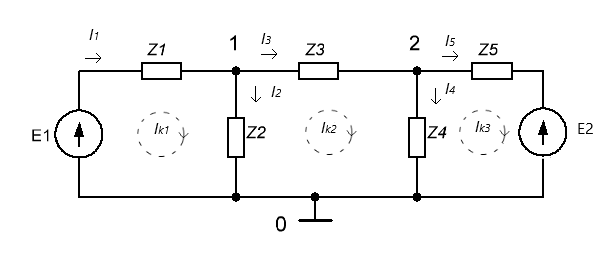Рис.1
Эта схема уже использовалась при рассмотрении метода контурных токов. Преобразуем данную схему, заменив сопротивления на проводимости, а ЭДС на эквивалентные генераторы токов:
Рис.2
Проводимости определяются как:

      Yi = 1/Zi

Токи эквивалентных генераторов тока:

      Ie1 = E1•Y1,

      Ie2 = E2•Y5.

Узловыми напряжениями называются напряжения U10 между узлами 1 и 0 и U20 между узлами 2 и 0 или в общем случае напряжения m-го узла относительно опорного 0-го узла. Для данной цепи рис. 2 система уравнений узловых напряжения, основанная на законах Ома и Кирхгофа, выглядит следующим образом:

      U10Y11 + U20Y12 = Ie1       (1)

      U10Y21 + U20Y22 = Ie2       (2)

Где:

Yij – т.н. узловые проводимости, которые определяются заданными проводимостями в ветвях Y1, … , Y5 следующим образом:

1) Т.н. узловые проводимости (т.е. примыкающие к данному узлу):

      Y11 = Y1 + Y2 + Y3 ,       Y22 = Y3 + Y4+ Y5

2) Т.н. общие проводимости (т.е. соединяющие два узла):

      Y12 = Y21 = Y3

Таким образом, мы имеем систему из двух линейных уравнений (1) – (2) с двумя неизвестными U10, U20.
Решив эту систему, т.е. определив U10, U20, мы сможем определить токи ветвей для данной цепи:

      I1 = (E1 - U10)/ R1
      I2 = U10/ R2
      I3 = (U10 - U20) /R3
      I4 = U20/R4
      I5 = (U20 - E2)/ R5

В матричной форме система уравнений n – го порядка , где n – число узлов за минусом 0-го, записывается следующим образом:

      Ig = Y•U       (4)

где Ig – вектор-столбец из элементов Ig1, Ig2, … , Ign. Каждый элемент Igk - это в общем случае алгебраическая сумма генераторных токов Ie входящих (исходящих) для данного узла. Причём Ie берётся со знаком плюс если он направлен в узел и со знаком минус в противном случае;
U – вектор-столбец из элементов U10, U20, … , Un0;
Y – матрица проводимостей из элементов Yij, причем при i ≠ j перед Yij ставится минус:
В общем случае для системы из n-узлов:

Y =
| Y11 −Y12 ... −Y1n |
| −Y21 Y22 ... −Y2n |
| ... ... ... ... |
| −Yn1 −Yn2 ... Ynn |


Решение уравнения (4) имеет вид:

      U = Y-1•Ig,       (5)

где Y-1 – матрица, обратная матрице Y.

Ниже мы рассмотрим практические схемы и покажем как можно найти решение, используя возможности калькулятора KAN .

Практическая задача на постоянном токе

Рассмотрим следующую задачу . Ниже представлена схема из четырёх узлов: опорного узла 0 и трёх других 1, 2, 3: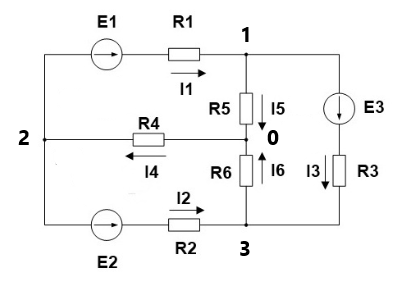
Рис. 3

Заметим, что опорный узел, как и все остальные выбираются произвольно.

Дано:

    1) значения ЭДС источников (контурные ЭДС):

      E1 = 80 В
      E2 = 50 В
      E3 = 60 В

   2) значения сопротивлений:

      R1 = 10 Ом
      R2 = 15 Ом
      R3 = 20 Ом
      R4 = 25 Ом
      R5 = 30 Ом
      R6 = 35 Ом

Преобразуем схему следующим ообразом:
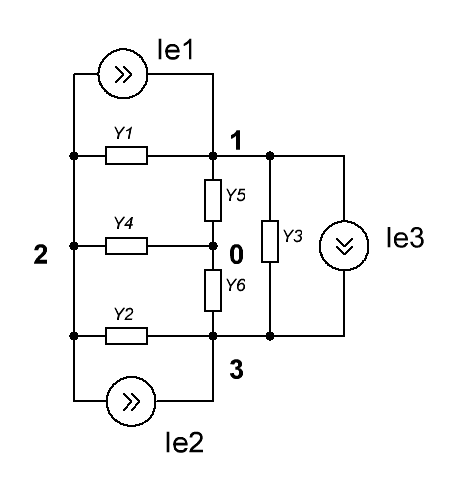Рис.4
Составим текст программы для данной задачи:

; Калькулятор KAN. http://калькулятор.нехаев.рф/calc/calculator.html
; Метод узловых напряжений. Постоянный ток
;задача - https://electroandi.ru/toe/metod/metod-konturnykh-tokov-reshenie-zadach.html
mas: Y[3,3], Yrev[3,3], U[3,1], Ig[3,1]; декларирование массивов для элементов матриц
;--------------------- ДАНО: --------------------------------
; значения ЭДС источников (контурные ЭДС)
E1 = 80
E2 = 50
E3 = 60
; значения сопротивлений
R1 = 10
R2 = 15
R3 = 20
R4 = 25
R5 = 30
R6 = 35
;------------------------- РАСЧЁТ -------------------------------
format(dec,5) ; формат выводимых чисел
; значение узловых проводимостей
Y1 = 1/R1
Y2 = 1/R2
Y3 = 1/R3
Y4 = 1/R4
Y5 = 1/R5
Y6 = 1/R6
; расчет элементов матрицы узловых проводимостей
Y11 = Y1 + Y5 + Y3
Y22 = Y1 + Y4 + Y2
Y33 = Y2 + Y6 + Y3
Y12 = Y1
Y21 = Y12
Y13 = Y3
Y31 = Y13
Y23 = Y2
Y32 = Y23
; матрица узловых проводимостей
Y = |
Y11 -Y12 -Y13
-Y21 Y22 -Y23
-Y31 -Y32 Y33
|
; токи эквивалентных генераторов тока
Ie1 = E1*Y1
Ie2 = E2*Y2
Ie3 = E3*Y3
;узловые генераторные токи
Ig1 = Ie1 - Ie3
Ig2 = - Ie1 - Ie2
Ig3 = Ie2 + Ie3
; матрица узловых генераторных токов
Ig = |
Ig1
Ig2
Ig3
|
Yrev = revM(Y) ; вычисление реверсивной матрицы узловых проводимостей
U = |Yrev*Ig| ; вычисление узловых напряжений (решение системы уравнений)
;узловые напряжения
U10 = U[1,1] = 16.14849
U20 = U[2,1] = -36.58159
U30 = U[3,1] = 32.37432
;расчёт токов в ветвях
I1 = (E1 - U10 + U20)/R1 = 2.72699
I2 = (E2 - U30 + U20)/R2 = -1.26373
I3 = (E3 - U30 + U10)/R3 = 2.18871
I4 = U20/R4 = -1.46326
I5 = U10/R5 = 0.53828
I6 = U30/R6 = 0.92498
;------------ ПРОВЕРКА РАСЧЁТА ---------------
;----------- ЭНЕРГОБАЛАНС -------------
Pe = E1*I1 + E2*I2 + E3*I3 = 286.29544
Pi = I1^2*R1 + I2^2*R2 + I3^2*R3 + I4^2*R4 + I5^2*R5 + I6^2*R6 = 286.29544


Если ввести данную программу в окно калькулятора, то получим значения, которые подставятся при вычислении непосредственно в тексте программы после второго знака равно. Если изменить исходные значения ЭДС и сопротивлений, изменятся и расчётные значения.
Для проверки правильности расчёта вычисляется баланс мощностей. Суммарная мощность, затрачиваемая от источников Pe, должна быть равна суммарной мощности, выделяемой на пассивных элементах цепи Pi. В данном случае, так оно и есть.

Листинг программы на Mathcad доступен здесь

Практическая задача на переменном токе

В качестве практического применения метода узловых напряжений на переменном токе рассмотрим следующую схему.
Рис.5

Данная схема представляет собой фильтр нижних частот (ФНЧ), рассмотренный в разделе . Для частоты среза 100 Гц ФНЧ имеет следующие значения:

R1 = 318 Ом – сопротивление источника
Rn = R1 = 318 Ом – сопротивление нагрузки
C1 = C2 = 5 мкФ (5Е-6 Ф)
L1 = 1.013 Гн

В том же разделе была вычислена амплитудно-частотная характеристика (АЧХ) данного фильтра по аналитической формуле. Здесь с этой же целью мы применим метод узловых напряжений.

Для начала рассчитаем схему на одной частоте f = 100 Гц.
Обозначим :
ω = 2πf – круговая частота

Для схемы рис. 1, которая полностью соответствует схеме на рис. 5, сопротивления ветвей будут рассчитываться как:

Z1 = R1
Z2 = - i/( ωC1)
Z3 = iωL1
Z4 = Z2
Z5 = Rn

Как видим значения сопротивлений источника R1 и нагрузки Rn – действительные числа, а сопротивлений Z2, Z3, Z4 – мнимые, где i – мнимая единица.
Программа расчета данной цепи для калькулятора KAN приведена ниже:
; Калькулятор KAN.
; метод узловых напряжений. Переменный ток
mas: Y[2,2], Yrev[2,2], U[2,1], Ig[2,1]; декларирование массивов для элементов матриц
;--------------------- ДАНО: --------------------------------
C1 = 5E-6
C2 = C1
L = 1.013
f = 100 ; частота
w = 2*pi*f ; круговая частота
R1 = 318 ; сопротивление источника
Z1 = R1
Z2 = -!/(w*C1); комплексное сопротивление ёмкости C1
Z3 = !(w*L); комплексное сопротивление индуктивности L
Z4 = Z2
Z5 = R1 ; сопротивление нагрузки
; значения ЭДС источников
E1 = 1
;------------------------- РАСЧЁТ -------------------------------
format(dec,5) ; формат выводимых чисел
; значение узловых проводимостей
Y1 = 1/Z1
Y2 = 1/Z2
Y3 = 1/Z3
Y4 = 1/Z4
Y5 = 1/Z5
; расчет элементов матрицы узловых проводимостей
Y11 = Y1 + Y2 + Y3
Y22 = Y3 + Y4 + Y5
Y12 = Y3
Y21 = Y3
; матрица узловых проводимостей
Y = |
Y11 -Y12
-Y21 Y22
|
Ig1 = E1*Y1 ; ток эквивалентного генератора тока
; матрица генераторных токов
Ig = |
Ig1
0
|
Yrev = revM(Y) ; вычисление реверсивной матрицы узловых проводимостей
U = |Yrev*Ig| ; вычисление узловых напряжений (решение системы уравнений)
valM(U) : U = |0.75024-!0.2499, -0.24976-!0.2501|
; расчет напряжения на сопротивлении нагрузки
Un = U[2,1] = -0.24976-!0.2501
; расчет коэффициента передачи (передаточная функция цепи)
K = Un/E1 = -0.24976-!0.2501 ; модуль коэффициента передачи
K = modC(K) = 0.35346
K_db = 20*lg(K) = -9.03332 ; модуль коэффициента передачи в децибелах


Пояснения даны в виде комментариев. Комплексное число вида a + ib записывается на языке KAN как a + !b. Как видно из текста программы модуль коэффициента передачи на частоте 100 Гц составил около -9 дБ, что соответствует результату, полученному в разделе расчета АЧХ для этой частоты.

Особо поясним строку:

E1 = 1.

Эта запись не означает, что взято постоянное напряжение равное 1 вольту. В данном случае напряжение переменное и в комплексной форме записывается как:

E1 = Aeiφ,

где A – амплитуда, а φ = ωt + φ0 - мгновенная фаза гармонического сигнала. Причем A = 1, φ = 0. Запись E1 = 1, соответствует этому случаю. Если бы мы рассматривали случай с ненулевой фазой, например φ = π/4 и амплитудой 1 вольт, мы данную строку записали бы так:

E1 = exp(!pi/4)

что соответствовало бы математической записи гармонического сигнала в комплексном виде:

E1 = eiπ/4

Соответственно комплексные значения токов и других комплексных величин получились бы другими, тогда как их модули, а так же модуль передаточной функции K и его логарифмическое значение K_db остались бы неизменными.

Данную программу нетрудно применить для произвольной ЛЭЦ, заменив размерность матриц (в директиве mas: число 2 заменяется на другое число узлов) и подставив соответствующие значения сопротивлений ветвей Zm и ЭДС Ek.

В приведённой выше программе, помимо расчета токов ветвей цепи рис. 5, было получено значение АЧХ фильтра в одной точке f=100 Гц, равное примерно -9 дБ.

Листинг программы на Mathcad доступен здесь
Теперь модифицируем программу, чтобы, используя метод узловых напряжений, рассчитать АЧХ ФНЧ, представленного на рис. 5, в диапазоне частот.


; Калькулятор KAN.
; метод узловых напряжений. Расчёт АЧХ фильтра нижних частот
mas: Y[2,2], Yrev[2,2], U[2,1], Ig[2,1]; декларирование массивов для элементов матриц
;--------------------- ДАНО: --------------------------------
C1 = 5E-6
C2 = C1
L = 1.013
R1 = 318 ; сопротивление источника
; значения ЭДС источников
E1 = 1
; матрица узловых проводимостей
Y = |
Y11 -Y12
-Y21 Y22
|
; матрица генераторных токов
Ig = |
Ig1
0
|
;------------------------- РАСЧЁТ -------------------------------
[f = 0:1000,10 ; цикл по частоте fmin:fmax, df
{f=0 f = 0.0001} ; для исключения деления на 0 при вычислении Z2
w = 2*pi*f ; круговая частота
;сопротивления ветвей
Z1 = R1
Z2 = -!/(w*C1)
Z3 = !(w*L)
Z4 = Z2
Z5 = R1 ; сопротивление нагрузки
; значение узловых проводимостей
Y1 = 1/Z1
Y2 = 1/Z2
Y3 = 1/Z3
Y4 = 1/Z4
Y5 = 1/Z5
; расчет элементов матрицы узловых проводимостей
Y11 = Y1 + Y2 + Y3
Y22 = Y3 + Y4 + Y5
Y12 = Y3
Y21 = Y3
;
Yrev = revM(Y) ; вычисление реверсивной матрицы узловых проводимостей
Ig1 = E1*Y1
U = |Yrev*Ig| ; вычисление узловых напряжений (решение системы уравнений)
; напряжение на сопротивлении нагрузки
Un = U[2,1]
; расчет коэффициента передачи (передаточная функция цепи)
K = Un/E1
K = modC(K) ; модуль коэффициента передачи
K_db = 20*lg(K); модуль коэффициента передачи в децибелах
val(f, K_db); вывод значений АЧХ в таблицу и на график
]; завершение цикла
grafY(-50,0) ; задание пределов по оси Y
grafX(0,500) ; задание пределов по оси X


Теперь расчёт осуществляется в цикле изменением частоты f. Если ввести данную программу в окно калькулятора, то получим таблицу значений АЧХ K_db в децибелах и график, который представлен ниже.

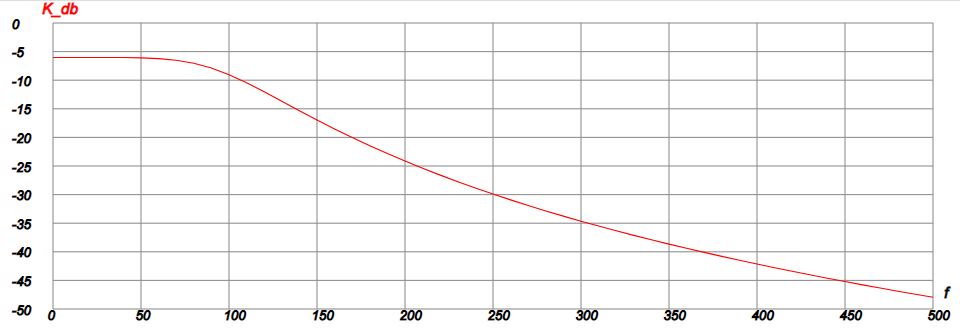Рис.6

Сравнивая этот график с графиком, полученным в другом разделе и совсем другим способом, приходим к выводу, что они совпадают.
  Обратная связь: 
alexander.nekhaev53@gmail.com 		  Поддержать проект   Заказать расчет