На главную     ↑ Выше

Метод наложения
(метод суперпозиций)

Элементы теории


На страницах:

Расчёт амплитудно-частотных характеристик

Расчёт фазочастотных характеристик

был рассмотрен относительно простой метод расчёта амплитудно- и фазо- частотных характеристик пассивных четырёхполюсников с одним источником напряжения на входе, а именно метод делителей напряжения Но, во-первых источников может быть несколько, а во-вторых, в схеме могут присутствовать активные элементы, например, операционные усилители в активных фильтрах с различными обратными связями. В этом случае также можно использовать как метод контурных токов так и метод узловых напряжений. Однако есть более простой способ, который мы и рассмотрим.
Здесь мы имеем дело с линейными системами, которые примечательны тем, что результат воздействия на систему нескольких источников равен сумме результатов воздействия на неё отдельных источников. А это означает, что мы можем применить метод делителей напряжения для каждого источника по отдельности и сложить результат.
Рассматривая метод делителей напряжения мы использовали обобщённую схему линейного четырёхполюсника как на рис. 1
Рис. 1


и пришли к выводу, что комплексный коэффициент передачи для этой схемы равен произведению комплексных коэффициентов передачи отдельных звеньев:

      K = K1•K2•K3...•Kn          (1)

при этом расчет каждого Ki сводится к расчету параллельных и последовательных сопротивлений.
Дополним эту схему источниками напряжения в каждой вертикальной ветви.
Рис. 2

В соответсвии с принципом наложения (суперпозиции) напряжение в точке n будет равно сумме напряжений от отдельных источников:

      Un = K•E1 + K10•E10 + K20•E20 + ... + Kn0•En0

Как рассчитать К мы уже знаем: это формула (1). Т.е. мы как бы закорачиваем все остальные источники напряжения, кроме E1. Для нахождения K10 поступаем аналогично, закоротив все источники, кроме E10. И так поступаем для всех источников в данной схеме.
Для полной общности можно было бы расположить источники напряжений так же и в горизонтальных ветвях схемы, но, во-первых, такой случай встречается крайне редко (всё же источники одним концом обычно заземляются), а, во-вторых, не составит труда рассчитать коэффициенты и для этого случая.
Заметим также, что на месте источников напряжения могли бы быть источники токов. В этом случае мы бы не закорачивали, а наоборот как бы убирали источники полагая, что на их месте возникает разрыв цепи.

Практическое применение метода наложения


На странице Расчёт активных фильтров нижних и верхних частот мы рассмотрели расчет активных фильтров нижних и верхних частот, изображённых на следующей схеме:
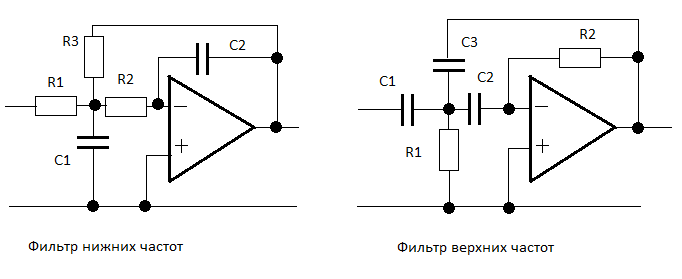Рис. 3


а также выполнили их моделирование в LTspice. Со всеми номиналами оба фильтра представлены ниже в "импортных" обозначениях:

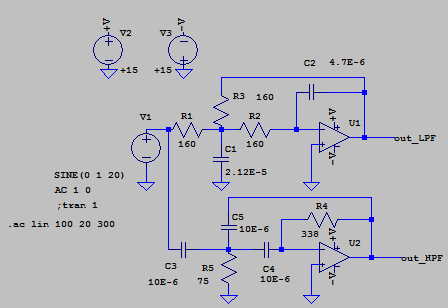Рис. 4


Применим метод наложения к расчету данных схем. На рис. 5 представлена обощённая схема, сответствующая обоим фильтрам.

Рис. 5


Заменим схему на операционном усилители на эквивалнетную как принято в теории:

Рис. 5


и найдём её коэффициент передачи

u2 = u2(e1) + u2(e2)
u2(e1) = e1•K1•Ko
u2(e2) = e2•K2•Ko,
а поскольку e2 = u2
u2(e2) = u2•K2•Ko,
выразим коэффициенты через сопротивления
K1 = Z20/(Z20 + Z1),
Z20 = Z5||Z2||Z3,
Ko = - Z4/Z2
K2 = Z20_/(Z20_ + Z1),
Z20_ = Z5||Z2||Z1
делее после несложных преобразований
u2 = e1•K1•Ko + u2•K2•Ko
u2•(1-K2•Ko) = e1•K1•Ko
получим общий коэффициент передачи данной схемы
K = u2/e1 = K1•Ko/(1-K2•Ko)

Теперь напишем программу для калькулятора КАН, взяв номиналы резисторов и конденсаторов из схемы рис. 4

; для ФНЧ
f = 10
f2 = 500
[
w = 2*pi*f
R1 = 160
R2 = R1
R3 = 160
C1 = 2.12E-5
C2 = 4.7E-6
Z1 = R1
Z2 = R2
Z3 = R3
Z4 = 1/(!(w*C2))
Z5 = 1/(!(w*C1))
Z20 = parC(parC(Z5,Z2),Z3)
Z20_ = parC(parC(Z1,Z5),Z2)
K1 = Z20/(Z1 + Z20)
K2 = Z20_/(Z3 + Z20_)
Ko = -Z4/Z2
K = modC(K1*Ko/(1 - K2*Ko))
val(f,K)
f = f + 10
{f>f2 exit}
]
grafX(0,500)
grafY(0,1)


Скопировав программу в окно, калькулятора, получим таблицу и график АЧХ фильтра нижних частот.

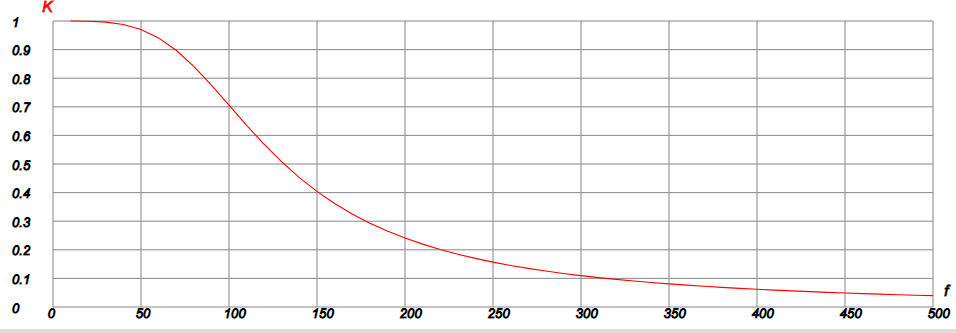Рис. 6


Аналогично поступим для ФВЧ.

; для ФВЧ
f = 10
f2 = 500
[
w = 2*pi*f
R5 = 75
R4 = 338
C3 = 10E-6
C4 = C3
C5 = C3
Z1 = 1/(!(w*C3))
Z2 = 1/(!(w*C4))
Z3 = 1/(!(w*C5))
Z4 = R4
Z5 = R5
Z20 = parC(parC(Z5,Z2),Z3)
Z20_ = parC(parC(Z1,Z5),Z2)
K1 = Z20/(Z1 + Z20)
K2 = Z20_/(Z3 + Z20_)
Ko = -Z4/Z2
K = modC(K1*Ko/(1 - K2*Ko))
val(f,K)
f = f + 10
{f>f2 exit}
]
grafX(0,500)
grafY(0,1)


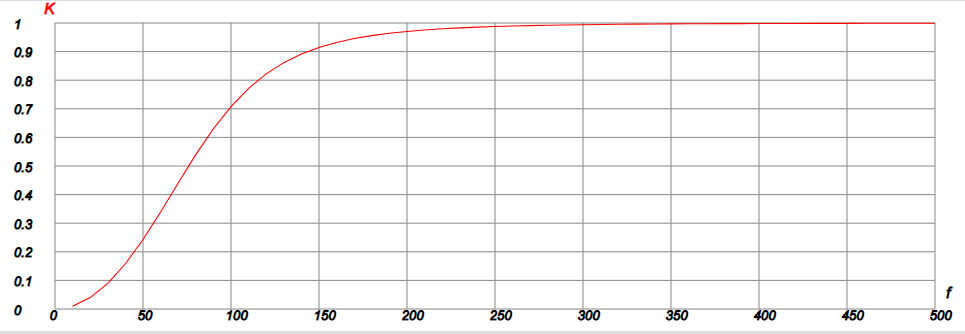Рис. 7



  Обратная связь: 
alexander.nekhaev53@gmail.com 		  Поддержать проект   Заказать расчет