| На главную ↑ Выше |
Расчет LC-фильтра нижних частот Чебышева |
| Заказать расчет |
На данной странице рассмотрены вопросы расчёта ФНЧ Чебышева на калькуляторе КАН.
Пакет Mathcad-программ для расчета ФНЧ Чебышева доступен по ссылке
Амплитудно-частотная характеристика
ФНЧ Чебышева (фильтр с аппроксимацией прямоугольной характеристики с применением полиномов Чебышева) обеспечивает более крутой спад амплитудно-частотной характеристики (АЧХ ) за частотой среза, нежели ФНЧ Баттерворта при той же сложности. Однако, «платой» за это является волнообразный вид АЧХ ниже частоты среза и, кроме того, бОльшая нелинейность фазо-частотной характеристики, что существенно для фильтрации некоторых видов сигналов, в частности, цифровых.Аналитическая зависимость коэффициента передачи данного фильтра K(f) имеет вид:
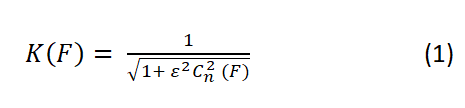
Где
F = f/fc нормированная частота
f – частота,
fc – частота среза,
n – порядок фильтра
ε – параметр, задающий неравномерность в полосе пропускания (F<=1)
Cn – полином Чебышева n-го порядка.
В тригонометрическом виде полиномы Чебышева записываются следующим образом:
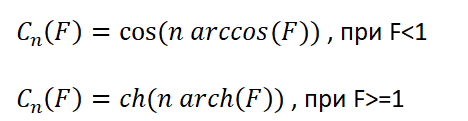
Где ch и arch – прямой и обратный гиперболический косинусы.
Для того, чтобы построить графики АЧХ в децибеллах, воспользуемся калькулятором KAN.
Программа расчета для случаев n = 1, 2, 3.
Фрагмент программы показан ниже:
Кликните по нему, чтобы запустить программу.
В дальнейшем используйте данную программу, подставляя свои значения.
Как сохранять программу и её результаты описано здесь.
Графики K(F) для n = 1, 2 , 3 (K1, K2, K3) представлены на рис 1.
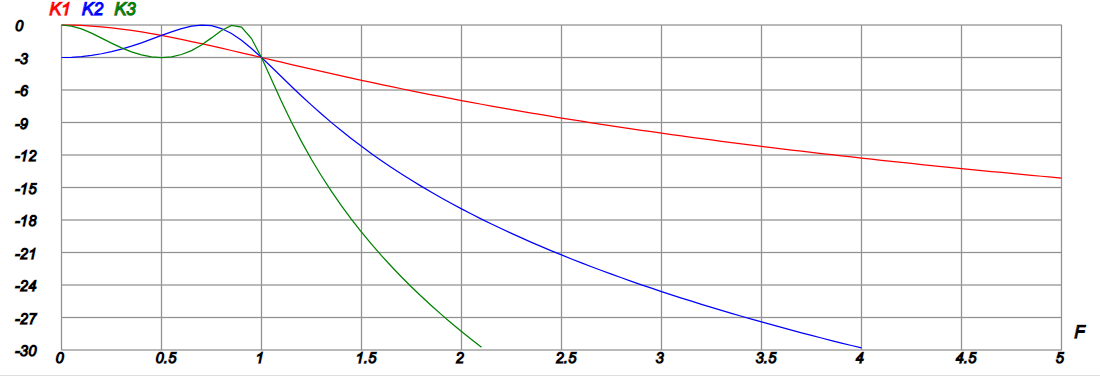
Рис. 2
Определение порядка многозвенного фильтра Чебышева
Перейдем к общему случаю, когда требуется произвести расчёт при заданных значениях крутизны спада АЧХ. Для этого нужно определить порядок фильтра. Порядок фильтра n задает величину спада АЧХ в полосе подавления (непропускания). Соответственно он определяет и сложность фильтра. Для расчёта фильтра нижних частот принято задавать следующие параметры:fc – частота среза фильтра и, соответственно, неравномерность АЧХ в полосе пропускания a1.
fr – частота, с которой начинается заданное ослабление фильтра a2.
Формулы для определения порядка фильтра Чебышева даны в технической литературе (см. например [2])
Мы же опять воспользуемся калькулятором KAN и приведем готовую программу.
В качестве примера определим порядок фильтра для ФНЧ Баттерворта (для сравнения) и ФНЧ Чебышева, задав следующие значения:
fc = 100 Гц
fr = 130 Гц
a1 = 3 дБ
a2 = 20 дБ
; калькулятор KAN
;определение порядка ФНЧ Баттерворта и Чебышева
; теория Джонсон с.12
;------------ ДАНО: --------------------------
f1 = 100; частота среза (верхняя частота, на которой затухание равно а1)
f2 = 130; нижняя частота полосы непропускания (частота выше которой затухание >= a2)
a1 = 3; неравномерность затухания в полосе пропускания
a2 = 20; затухание в полосе непропускания
;----------- РАСЧЁТ параметров ----------------
q = f2/f1
; ФНЧ Баттерворта
n = ln(10^(a2/10) - 1)/(2*ln(q))
n = int(n) + 1
n_batt = n ; порядок ФНЧ Баттерворта, удовлетворяющий условиям задачи
; фНЧ Чебышева
x = sqr((10^(a2/10) - 1)/(10^(a1/10)- 1))= 9.97353
ch = arch(x)
x = q
zn = arch(x)
n = ch/zn
n = int(n) + 1 = 4
n_cheb = n ; порядок ФНЧ Чебышева, удовлетворяющий условиям задачи
;----------------- РЕЗУЛЬТАТЫ РАСЧЁТА ----------------------
val(n_batt, n_cheb): n_batt = 9, n_cheb = 4
;определение порядка ФНЧ Баттерворта и Чебышева
; теория Джонсон с.12
;------------ ДАНО: --------------------------
f1 = 100; частота среза (верхняя частота, на которой затухание равно а1)
f2 = 130; нижняя частота полосы непропускания (частота выше которой затухание >= a2)
a1 = 3; неравномерность затухания в полосе пропускания
a2 = 20; затухание в полосе непропускания
;----------- РАСЧЁТ параметров ----------------
q = f2/f1
; ФНЧ Баттерворта
n = ln(10^(a2/10) - 1)/(2*ln(q))
n = int(n) + 1
n_batt = n ; порядок ФНЧ Баттерворта, удовлетворяющий условиям задачи
; фНЧ Чебышева
x = sqr((10^(a2/10) - 1)/(10^(a1/10)- 1))= 9.97353
ch = arch(x)
x = q
zn = arch(x)
n = ch/zn
n = int(n) + 1 = 4
n_cheb = n ; порядок ФНЧ Чебышева, удовлетворяющий условиям задачи
;----------------- РЕЗУЛЬТАТЫ РАСЧЁТА ----------------------
val(n_batt, n_cheb): n_batt = 9, n_cheb = 4
Можно скопировать данную программу в окно калькулятора и, подставляя другие значения, использовать её в своих расчетах.
Из результатов расчета видно, что одинаковые исходные условия для ФНЧ Чебышева выполняются при n = 4, тогда как для ФНЧ Баттерворта при n = 9.
Заметим, что сложность обоих типов ФНЧ при данном n одинакова и прямо пропорциональна порядку фильтра. Следовательно, при заданных выше условиях ФНЧ Чебышева будет почти в 2 раза проще ФНЧ Баттерворта.
Расчет LC-фильтра нижних частот Чебышева
Перейдем к реализации ФНЧ Чебышева. Причём реализаций может быть множество, например, на LC-элементах, на операционных усилителях, на переключаемых конденсаторах, на цифровых вычислительных устройствах и др. Здесь мы ограничимся реализацией на LC- элементах, т.е. на катушках индуктивности и конденсаторах. Опуская математическую сторону вопроса (см. [1]), приведем реализацию ФНЧ Чебышева на LC-элементах. Для n = 5 схема выглядит следующим образом: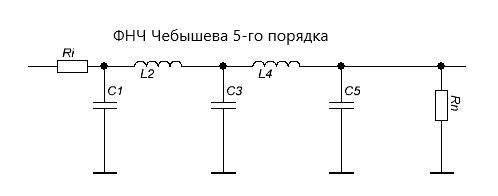
Рис. 3 ФНЧ Чебышева 5-го порядка на основе П- образных LC-звеньев
Обратите внимание, что нумерация элементов общая для L и C. Так удобно для расчетов. Закономерность построения схем достаточно простая, чтобы построить фильтр любого порядка. Заметим также, что для ФНЧ Чебышева (как и для ФНЧ Баттерворта ) порядок фильтра равен количеству LC-элементов. Сопротивления источника Ri и нагрузки Rn берутся не произвольным образом. Их значения связаны с величинами элементов L и C. При произвольных значениях Ri и Rn фильтр будет не согласован и его АЧХ будет отличаться от желаемой. Заметим также, что на нулевой частоте схема вырождается в простой резистивный делитель напряжения на резисторах Ri и Rn.
В теоретической литературе принято рассчитывать фильтр предварительно для значений Ri = 1 Ом и
рад/сек (соответствует 
Гц ). Такой фильтр называется нормированным. В [1] приведены формулы для расчёта нормированного ФНЧ Чебышева. На основе этих формул составлена программа для Фрагмент программы показан ниже:
Кликните по нему, чтобы запустить программу.
В дальнейшем используйте данную программу, подставляя свои значения.
Как сохранять программу и её результаты описано здесь.
Получите результат в виде таблицы:
---------------- Таблица данных ------------ стр. k C L 1 1.0000E+0 5.5406E-6 0.0000E+0 2 2.0000E+0 0.0000E+0 1.2126E+0 3 3.0000E+0 7.2217E-6 0.0000E+0 4 4.0000E+0 0.0000E+0 1.2126E+0 5 5.0000E+0 5.5406E-6 0.0000E+0
Значения C даны в Ф, значения L в Гн. Там, где значения равны нулю означает, что элементов с такими номерами k не существует. Изменяйте n, Ri и fc в данной программе для интересующих вас случаев.
Для проверки результатов расчёта желательно смоделировать полученный фильтр и убедиться в их правильности. Используем для этих целей бесплатный в настоящее время пакет моделирования MicroCap-12.
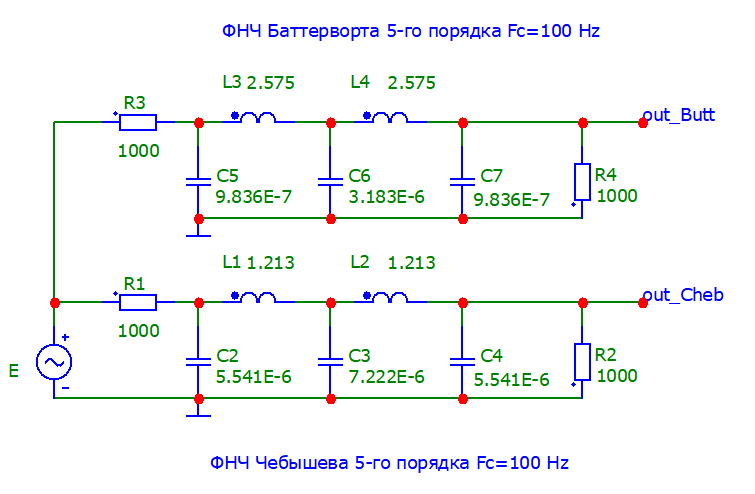
Рис. 4
На рис.4 изображены два фильтра: нижний: ФНЧ Чебышева 5-го порядка, расчитанный по приведённой выше программе, и верхний: ФНЧ Баттерворта также 5-го порядка, расчитанный в другом разделе.
Как видно схемы идентичны. Разница только в значениях элементов L и C.
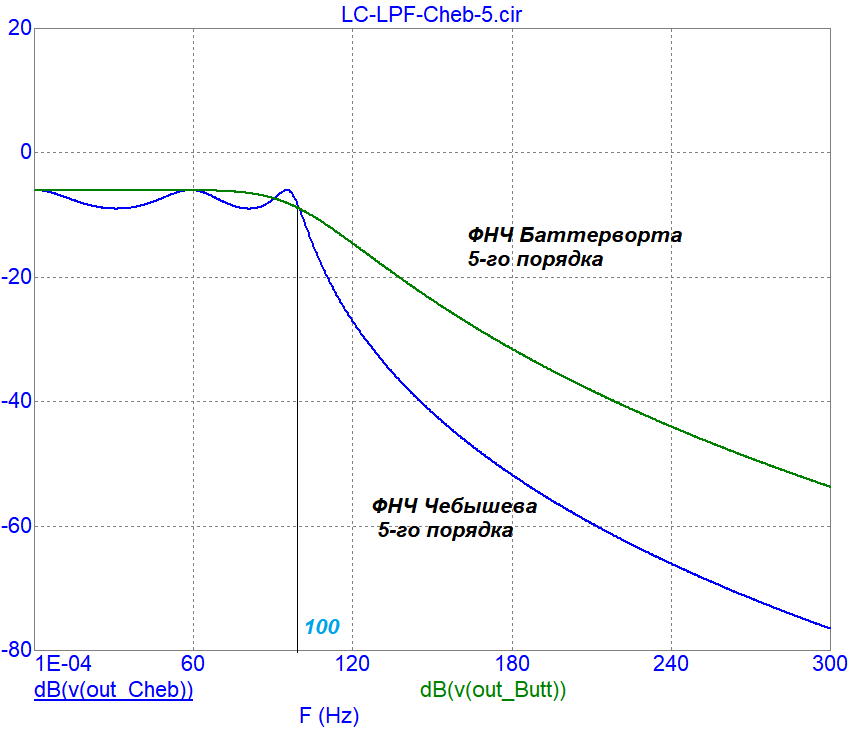
Ниже даны графики АЧХ обоих фильтров. Видно, что ФНЧ Чебышева имеет заметно более крутой спад за частотой среза 100 Гц.
Пакет Mathcad-программ для расчета ФНЧ Чебышева доступен по ссылке
Литература.
- Г. Лэм. Аналоговые и цифровые фильтры. Москва, Издательство Мир, 1982
- Д. Джонсон и др. Справочник по активным фильтрам.. Москва, Энергоатомиздат, 1983.
|
Обратная связь: alexander.nekhaev53@gmail.com |
|
Поддержать проект |
|
Заказать расчет |