На главную     ↑ Выше

Контрольная работа по расчёту электрической цепи

На страницах:

Метод контурных токов

Метод узловых напряжений

были рассмотрены основные методы расчёта электической цепи.
Ниже дан пример типовых заданий контрольных работ по расчёту электрической цепи на постоянном токе. Расчёт будем производить опираясь на методическое пособие [1]

Задание

1. Выберите и укажите на схеме произвольное направление токов во всех ветвях,
направление контуров. Пронумеруйте все узлы схемы.
2. Составьте по методу токов ветвей (МТВ) (он же метод законов Кирхгофа)
уравнения и рассчитайте токи всех ветвей схемы.
3. Проверьте баланс активной мощности.
4. Рассчитайте токи всех ветвей методом контурных токов (МКТ).
5. Рассчитайте токи всех ветвей методом узловых напряжений (МУН).

Пример решения:

Схема для задания и заданные величины:

     

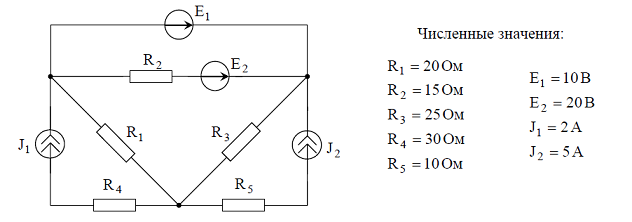
В матричном виде данная система уравнений будет выглядеть следующим образом

I * A = B

где
  

Решение в матричном виде выглядит так

I = A-1 * B

где A-1 – матрица, обратная матрицы A.

Ниже приведена программа для решения данного уравнения методом обращения матрицы на онлайн калькуляторе КАН. В программе также выполнен расчёт баланса мощностей.

;калькулятор КАН - http://калькулятор.нехаев.рф/calc/calculator.html
; метод токов ветвей (МТВ). 1-й и 2-й Законы Кирхгофа
mas: A[4,4], A_rev[4,4], B[4,1], I[4,1] ; декларация матриц (массивов)
;=================== ДАНО ===========================================
R1 = 20
R2 = 15
R3 = 25
R4 = 30
R5 = 10
E1 = 10
E2 = 20
J1 = 2
J2 = 5
;====================== РАСЧЕТ =======================================
A = | 0 -1 0 -1, 1 1 1 0, 0 -R1 R2 R3, 0 0 -R2 0|
dJ = -J1 - J2
dE = E1 - E2
B =| dJ, J1, E2, dE|
A_rev = revM (A) ; обращение матрицы
I = |A_rev*B| ; решение уравнения в матричном виде
; значения токов
valM(I) : I = |-2.33333, 3.66667, 0.66667, 3.33333|
I = I[1,1] = -2.33333
I1 = I[2,1] = 3.66667
I2 = I[3,1] = 0.66667
I3 = I[4,1] = 3.33333
;================= БАЛАНС МОЩНОСТЕЙ ====================================
; потребляемая мощность
P_pot = R1*I1^2 + R2*I2^2 + R3*I3^2 + R4*J1^2 + R5*J2^2 = 923.33333
; мощность, отбираемая от источников
U_J1 = I1*R1 + J1*R4 = 133.33333
U_J2 = I3*R3 + J2*R5 = 133.33333
P_ist = E1*I + E2*I2 + U_J1*J1 + U_J2*J2 = 923.33333


Расчет схемы методом контурных токов будем выполнять на основе методики, изложенной на этом сайте

Схему представим в следующем виде:

  

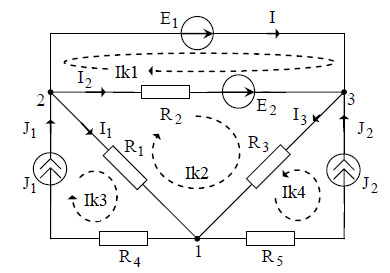
Заметим, что неизвестных контурных токов всего два: Ik1, Ik2, поскольку токи в двух других контурах известны: Ik3 = J1, Ik4 = J2, это означает, что мы будем иметь дело с уравнениями с двумя неизвестными.

Для данной цепи система уравнений контурных токов, основанная на законах Ома и Кирхгофа, выглядит следующим образом:
Ik1Z11 + Ik2Z12 = E1 (1)
Ik1Z21 + Ik2Z22 = 0 (2)
Где:

Ik1, Ik2 – контурные токи, которые предстоит найти.
Zij – т.н. контурные сопротивления, которые определяются заданными сопротивлениями в ветвях Z1, … , Z5 следующим образом:
1) Т.н. собственные контурные сопротивления: 
 
	Z11 = R2, 	Z22 = R1 + R2 + R3,
2) Т.н. общие контурные сопротивления 


	Z12 = Z21 = - R2
Таким образом, мы имеем систему из двух линейных уравнений (1) – (2) с двумя неизвестными Ik1, Ik2.
Решив эту систему, т.е. определив контурные токи Ik1, Ik2, мы сможем определить токи ветвей для данной цепи: 
 

	I = Ik1 
	I1 = J1 -  Ik2 
	I2 = Ik2 – Ik1 
	I3 = J2 + Ik2
Программа для данного случая приведена ниже:

;калькулятор КАН - http://калькулятор.нехаев.рф/calc/calculator.html
; Метод контурных токов
mas: Z[2,2], Z_rev[2,2], E[2,1], Ik[2,1] ; декларация матриц (массивов)
;=================== ДАНО ===========================================
R1 = 20
R2 = 15
R3 = 25
R4 = 30
R5 = 10
E1 = 10
E2 = 20
J1 = 2
J2 = 5
;====================== РАСЧЕТ =======================================
; матрица Z
Z11 = R2
Z12 = - R2
Z21 = Z12
Z22 = R1 + R2 + R3
Z = |
Z11 Z12,
Z21 Z22
|
; матрица E
Ek1 = E1 - E2
Ek2 = E2 + J1*R1 - J2*R3
E =| Ek1, Ek2|
; обращение матрицы
Z_rev = revM (Z)
; решение уравнения в матричном виде
Ik = |Z_rev*E|
; значения контурных токов
valM(Ik) : Ik = |-2.33333, -1.66667|
Ik1 = Ik[1,1]
Ik2 = Ik[2,1]
; значения токов ветвей
I = Ik1 = -2.33333
I1 = J1 - Ik2 = 3.66667
I2 = Ik2 - Ik1 = 0.66667
I3 = J2 + Ik2 = 3.33333

Как видим токи получились такими же, как и при МТВ

Наконец рассмотрим метод узловых напряжений. Примем узел 3 а качестве опорного.
Решение получается совсем простым, поэтому просто приведём фрагмент из методички [1].


  


Литература


[1] Панин Д.Н., Михайлов В.И.Методические указания к контрольной работе № 1 по I части курса «Основы теории цепей» для студентов заочного отделения. Поволжский государственный университет телекоммуникаций и информатики. Кафедра Теоретических основ радиотехники и связи. Самара 2009 г.

  Обратная связь: admin@нехаев.рф   Поддержать проект